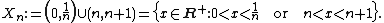“Interlocking interval topology”的意思、由来-开放百科全书

词条

Interlocking interval topology

释义

Construction
References

In mathematics, and especially general topology, the interlocking interval topology is an example of a topology on the set {{nowrap|1=S := R⁺ \\ Z⁺}}, i.e. the set of all positive real numbers that are not positive whole numbers.^[1] To give the set S a topology means to say which subsets of S are "open", and to do so in a way that the following axioms are met:^[2]

The union of open sets is an open set.
The finite intersection of open sets is an open set.
S and the empty set ∅ are open sets.

Construction

The open sets in this topology are taken to be the whole set S, the empty set ∅, and the sets generated by

The sets generated by X_n will be formed by all possible unions of finite intersections of the X_n.^[3]

References

1. ^Steen & Seebach (1978) pp.77 – 78
2. ^Steen & Seebach (1978) p.3
3. ^Steen & Seebach (1978) p.4

{{cite book | last1=Steen | first1=Lynn Arthur | author1-link=Lynn Arthur Steen | last2=Seebach | first2=J. Arthur Jr. | author2-link=J. Arthur Seebach, Jr. | title=Counterexamples in Topology | edition=2nd | year=1978 | publisher=Springer-Verlag | location=Berlin, New York | isbn=3-540-90312-7 | mr=507446 | zbl=0386.54001 }}

2 : General topology|Topological spaces

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。