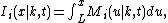“I-spline”的意思、由来-开放百科全书

词条

I-spline

释义

Definition
Computation
Applications
References

In the mathematical subfield of numerical analysis, an I-spline^[1]^[2] is a monotone spline function.

Definition

A family of I-spline functions of degree k with n free parameters is defined in terms of the M-splines M_i(x|k, t)

where L is the lower limit of the domain of the splines.

Since M-splines are non-negative, I-splines are monotonically non-decreasing.

Computation

Let j be the index such that t_j ≤ x < t_j+1. Then I_i(x|k, t) is zero if i > j, and equals one if j − k + 1 > i. Otherwise,

Applications

I-splines can be used as basis splines for regression analysis and data transformation when monotonicity is desired (constraining the regression coefficients to be non-negative for a non-decreasing fit, and non-positive for a non-increasing fit).

References

1. ^{{cite journal | title = On Polya frequency functions. IV. The fundamental spline functions and their limits | last=Curry | first =H.B. |author2=Schoenberg, I.J. | year=1966 | volume=17 | pages=71–107 | journal=J. Analyse Math. | doi = 10.1007/BF02788653}}
2. ^{{cite journal | last=Ramsay | first=J.O. | journal=Statistical Science | year = 1988 | volume=3 | pages=425–441 | title = Monotone Regression Splines in Action | jstor=2245395 | doi=10.1214/ss/1177012761 | issue=4}}

1 : Splines (mathematics)

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。