“K3 surface”的意思、由来-开放百科全书

词条

K3 surface

释义

Definition
Calculation of the Betti numbers
Properties
The period map
Projective K3 surfaces
Relation to string duality
Examples
History
See also
References
External links

{{quotebox
|quote=Dans la seconde partie de mon rapport, il s'agit des variétés kählériennes dites K3, ainsi nommées en l'honneur de Kummer, Kähler, Kodaira et de la belle montagne K2 au Cachemire.

In the second part of my report, we deal with the Kähler varieties known as K3, named in honor of Kummer, Kähler, Kodaira and of the beautiful mountain K2 in Kashmir.
|source=André {{harvtxt|Weil|1958|loc=p. 546}}, describing the reason for the name "K3 surface"
|width=30%}}

In mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.

In the Enriques–Kodaira classification of surfaces they form one of the four classes of surfaces of Kodaira dimension 0.

Together with two-dimensional complex tori, they are the Calabi–Yau manifolds of dimension two. Most complex K3 surfaces are not algebraic. This means that they cannot be embedded in any projective space as a surface defined by polynomial equations.

Definition

There are many equivalent properties that can be used to characterize a K3 surface. The only complete smooth surfaces with trivial canonical bundle are K3 surfaces and tori (or abelian varieties), so one can add any condition to exclude the latter to define K3 surfaces. Over the complex numbers the condition that the surface is simply connected is sometimes used.

There are a few variations of the definition: some authors restrict to projective surfaces, and some allow surfaces with Du Val singularities.

Calculation of the Betti numbers

Equivalently to the above definition, a K3 surface is defined as a surface S with trivial canonical bundle and irregularity . One has

and, from Serre duality,

Altogether, one obtains the Euler characteristic

On the other hand, the Riemann–Roch theorem (Noether's formula) reads

,

where is the i-th Chern class. Since is trivial, its first Chern class vanishes, hence .

Since hence 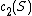is equal to the Euler number e(S) = b₀(S) − b₁(S) + b₂(S) − b₃(S) + b₄(S) and b₀(S) = b₄(S) = 1, b₁(S) = b₃(S) = 2q(S) = 0, we obtain b₂(S) = 22.

Properties

1. All complex K3 surfaces are diffeomorphic to one another (proved by Kunihiko Kodaira firstly). {{harvs|txt|last=Siu | first=Yum-Tong |authorlink=Yum-Tong Siu| year=1983}} showed that all complex K3 surfaces are Kähler manifolds. As a consequence of this and Shing-Tung Yau's solution to the Calabi conjecture, all complex K3 surfaces admit Ricci-flat metrics.

2. The (p,q)-th cohomology groups are indicated in the Hodge diamond{{Hodge diamond|style=font-weight:bold
| 1
| 0 | 0
| 1 | 20 | 1
| 0 | 0
| 1
}}

3. On , the cup product defines a lattice structure, called the K3 lattice, as described in the next section.

Because of the above properties, K3 surfaces have been studied extensively not only in algebraic geometry but also in Kac–Moody algebras, mirror symmetry and string theory. In particular, the lattice structure provides the modularity with the Néron–Severi group on it.

The period map

There is a coarse moduli space for marked complex K3 surfaces, a non-Hausdorff smooth analytic space of complex dimension 20. There is a period mapping and the Torelli theorem holds for complex K3 surfaces.

The set M of pairs consisting of a complex K3 surface S and a Kähler class of is in a natural way a real analytic manifold of dimension 60. There is a refined period map from M to a space KΩ⁰ that is an isomorphism. The space of periods can be described explicitly as follows:

L is the even unimodular lattice II_3,19.
Ω is the Hermitian symmetric space consisting of the elements of the complex projective space of that are represented by elements ω with (ω,ω) = 0, (ω,ω) > 0.
KΩ is the set of pairs (κ, [ω]) in (L⊗R, Ω) with (κ,E(ω)) = 0, (κ,κ) > 0.
KΩ⁰ is the set of elements (κ, [ω]) of KΩ such that (κd) ≠ 0 for every d in L with (d,d) = −2, (ω,d) = 0.

Projective K3 surfaces

If L is a line bundle on a K3 surface, the curves in the linear system have genus g, where

c₁²(L) = 2g − 2. A K3 surface with a line bundle L like this is called a K3 surface of genus g. A K3 surface may have many different line bundles making it into a K3 surface of genus g for many different values of g. The space of sections of the line bundle has dimension g + 1, so there is a morphism of the K3 surface to projective space of dimension g. There is a moduli space F_g of K3 surfaces with a primitive ample line bundle L with c₁²(L) =2g − 2, which is nonempty of dimension 19 for g ≥ 2. {{harvtxt|Mukai|2006}} showed that this moduli space F_g is unirational if g ≤ 13, and {{harvs | txt| last1=Gritsenko | first1=V. A. | last2=Hulek | first2=Klaus | last3=Sankaran | first3=G. K. | title=The Kodaira dimension of the moduli of K3 surfaces | doi=10.1007/s00222-007-0054-1 | mr=2336040 | year=2007 | journal=Inventiones Mathematicae | volume=169 | issue=3 | pages=519–567}} showed that it is of general type if g ≥ 63. {{harvtxt|Voisin|2008}} gave a survey of this area.

Relation to string duality

K3 surfaces appear almost ubiquitously in string duality and provide an important tool for the understanding of it. String compactifications on these surfaces are not trivial, yet they are simple enough for us to analyze most of their properties in detail. The type IIA string, the type IIB string, the E₈×E₈ heterotic string, the Spin(32)/Z2 heterotic string, and M-theory are related by compactification on a K3 surface. For example, the Type IIA compactified on a K3 surface is equivalent to the heterotic string compactified on 4-torus {{harvtxt|Aspinwall|1996}}.

Examples

A double cover of the projective plane branched along a non-singular degree 6 curve is a genus 2 K3 surface.
A Kummer surface is the quotient of a two-dimensional abelian variety A by the action a → −a. This results in 16 singularities, at the 2-torsion points of A. The minimal resolution of this quotient is a genus 3 K3 surface.
A non-singular degree 4 surface in P³ is a genus 3 K3 surface.
The intersection of a quadric and a cubic in P⁴ gives genus 4 K3 surfaces.
The intersection of three quadrics in P⁵ gives genus 5 K3 surfaces.
{{harvtxt|Brown|2007}} describes a computer database of K3 surfaces.

History

K3 surface was first discovered by Srinivasa Ramanujan in 1910s but remained unpublished,^[1]^[2] and was rediscovered by André {{harvtxt|Weil|1958}} who named them in honor of three algebraic geometers, Ernst Kummer, Erich Kähler and Kunihiko Kodaira, and the mountain K2 in Pakistan.

References

1. ^{{harvtxt|Ono|Trebat-Leder|2016}}
2. ^{{harvtxt|Ono|Trebat-Leder|2017}}

{{citation | first1=Ken | last1=Ono | first2=Sarah | last2=Trebat-Leder | title=The 1729 K3 surface | url=https://resnumtheor.springeropen.com/articles/10.1007/s40993-016-0058-2 | date=2016-10-17 | accessdate=2017-04-18 | publisher=Springer | journal=Research in Number Theory }}
{{citation | first1=Ken | last1=Ono | first2=Sarah | last2=Trebat-Leder | title=Erratum to: The 1729 K3 surface | url=https://resnumtheor.springeropen.com/articles/10.1007/s40993-017-0076-8 | date=2017-02-10 | accessdate=2017-04-18 | publisher=Springer | journal=Research in Number Theory }}
{{Citation|title=Compact Complex Surfaces|first= Wolf P.|last1= Barth|first2=Klaus|last2= Hulek|first3= Chris A.M. |last3=Peters|first4= Antonius |last4=Van de Ven |isbn=3-540-00832-2|year=2004|publisher=Springer|location=Berlin}}
{{Citation | last1=Beauville | first1=Arnaud | title=Bourbaki seminar, Vol. 1982/83 Exp 609 | url=http://www.numdam.org/item?id=SB_1982-1983__25__217_0 | publisher=Société Mathématique de France | location=Paris | series=Astérisque | mr=728990 | year=1983 | volume=105 | chapter=Surfaces K3 | pages=217–229}}
{{Citation | last1=Beauville | first1=A. | last2=Bourguignon | first2=J.-P. | last3=Demazure | first3= M. | title=Géométrie des surfaces K3: modules et périodes, Séminaires Palaiseau | publisher=Société Mathématique de France | location=Paris | series=Astérisque | mr=785216 | year=1985 | volume=126}}
{{Citation | last1=Brown | first1=Gavin | title=A database of polarized K3 surfaces | url=http://projecteuclid.org/euclid.em/1175789798 | mr=2312974 | year=2007 | journal=Experimental Mathematics | volume=16 | issue=1 | pages=7–20 | doi=10.1080/10586458.2007.10128983}}
{{Citation | last1=Burns | first1=Dan | last2=Rapoport | first2=Michael | title=On the Torelli problem for kählerian K-3 surfaces | url=http://www.numdam.org/item?id=ASENS_1975_4_8_2_235_0 | mr=0447635 | year=1975 | journal=Annales Scientifiques de l'École Normale Supérieure |series=Série 4 | volume=8 | issue=2 | pages=235–273}}
{{Citation | author1-link=Igor Dolgachev | last1=Dolgachev | first1=Igor V. | last2=Kondo | first2=Shigeyuki | editor1-last=Rolf-Peter Holzapfel | editor1-first=A. Muhammed Uludağ and Masaaki Yoshida | title=Arithmetic and geometry around hypergeometric functions | arxiv=math/0511051 | publisher=Birkhäuser | location=Basel, Boston, Berlin | series=Progr. Math. | isbn=978-3-7643-8283-4 | mr=2306149 | year=2007 | volume=260 | chapter=Moduli of K3 surfaces and complex ball quotients | pages=43–100|bibcode = 2005math.....11051D }}
{{Citation | last1=Gritsenko | first1=V. A. | last2=Hulek | first2=Klaus | last3=Sankaran | first3=G. K. | title=The Kodaira dimension of the moduli of K3 surfaces | doi=10.1007/s00222-007-0054-1 | mr=2336040 | year=2007 | journal=Inventiones Mathematicae | volume=169 | issue=3 | pages=519–567|arxiv = math/0607339 |bibcode = 2007InMat.169..519G }}
{{citation|series= Cambridge Studies in Advanced Mathematics|volume= 158

|publisher= Cambridge University Press|year= 2016
|isbn= 978-1107153042|title=Lectures on K3 surfaces|first= Daniel |last=Huybrechts}}

{{Citation | last1=Mukai | first1=Shigeru | author1-link=Shigeru Mukai | title=Moduli spaces and arithmetic geometry | publisher=Math. Soc. Japan | location=Tokyo | series=Adv. Stud. Pure Math. | mr=2310254 | year=2006 | volume=45 | chapter=Polarized K3 surfaces of genus thirteen | pages=315–326}}
{{springer|title=K3 surface|id=k/k055040|first=A.N. |last=Rudakov}}
{{Citation | last1=Pjateckiĭ-Šapiro | first1=I. I. | author1-link=Ilya Piatetski-Shapiro | last2=Šafarevič | first2=I. R. | title=Torelli's theorem for algebraic surfaces of type K3 | doi= 10.1070/IM1971v005n03ABEH001075 | mr=0284440 | year=1971 | journal= Math Ussr Izv | volume=5 | issue=3 | pages=547–588|bibcode = 1971IzMat...5..547P }}
{{Citation | last=Siu | first=Yum-Tong |authorlink=Yum-Tong Siu| title=Every K3 surface is Kähler | doi=10.1007/BF01393829 | mr=707352 | year=1983 | journal=Inventiones Mathematicae | volume=73 | issue=1 | pages=139–150|bibcode = 1983InMat..73..139S }}
{{Citation | last1=Voisin | first1=Claire | title=Géométrie des espaces de modules de courbes et de surfaces K3 (d'après Gritsenko-Hulek-Sankaran, Farkas-Popa, Mukai, Verra, et al.) | url=http://www.math.polytechnique.fr/~voisin/Articlesweb/Exp.981.C.Voisin.pdf | series=Séminaire Bourbaki. 2006/2007. Exp 981 | isbn=978-2-85629-253-2 | mr=2487743 | year=2008 | journal=Astérisque | issue=317 | pages=467–490}}
{{Citation | last1=Weil | first1=André | author1-link=André Weil | title=Scientific works. Collected papers | publisher=Springer-Verlag | location=Berlin, New York | isbn=978-0-387-90330-9 | mr=537935 | year=1958 | volume= II | chapter=Final report on contract AF 18(603)-57 | pages=390–395, 545–547}}
{{citation |first=Paul |last=Aspinwall |title=K3 Surfaces and String Duality |year=1996 |eprint=hep-th/9611137 }}

External links

[https://web.archive.org/web/20140222023430/http://grdb.lboro.ac.uk/ Graded Ring Database homepage] for a catalog of K3 surfaces
The Geometry of K3 surfaces, by David Morrison
K3 database for the Magma computer algebra system

4 : Algebraic surfaces|Complex surfaces|Differential geometry|String theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。