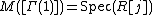“J-line”的意思、由来-开放百科全书

In the study of the arithmetic of elliptic curves, the j-line over any ring R is the coarse moduli scheme attached to the moduli problem Γ(1)]:^[1]

with the j-invariant normalized a la Tate: j = 0 has complex multiplication by Z[ζ₃], and j = 1728 by Z[i].

The j-line can be seen as giving a coordinatization of the classical modular curve of level 1, X₀(1), which is isomorphic to the complex projective line.^[2]

References

1. ^{{citation | last1 = Katz | first1 = Nicholas M. | author1-link = Nick Katz | last2 = Mazur | first2 = Barry | author2-link = Barry Mazur | isbn = 0-691-08349-5 | mr = 772569 | page = 228 | publisher = Princeton University Press, Princeton, NJ | series = Annals of Mathematics Studies | title = Arithmetic moduli of elliptic curves | url = https://books.google.com/books?id=M1IT0J_sPr8C&pg=PA228 | volume = 108 | year = 1985}}.
2. ^{{citation | last = Gouvêa | first = Fernando Q. | authorlink = Fernando Q. Gouvêa | contribution = Deformations of Galois representations | mr = 1860043 | pages = 233–406 | publisher = Amer. Math. Soc., Providence, RI | series = IAS/Park City Math. Ser. | title = Arithmetic algebraic geometry (Park City, UT, 1999) | volume = 9 | year = 2001}}. See in particular [https://books.google.com/books?id=PgHjLgIVidgC&pg=PA378 p. 378].