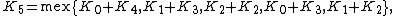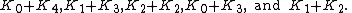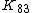1. Rules

2. History

3. Analysis

4. Applications

5. Computational complexity

6. See also

7. References

Kayles is a simple impartial game in combinatorial game theory. Using the notation of octal games, Kayles is denoted 0.77.

Rules

Kayles is played with a row of tokens, which represent bowling pins. The row may be of any length. The two players alternate; each player, on his or her turn, may remove either any one pin (a ball bowled directly at that pin), or two adjacent pins (a ball bowled to strike both). Under the normal play convention, a player loses when he or she has no legal move (that is, when all the pins are gone). The game can also be played using misère rules; in this case, the player who cannot move wins.

History

Kayles was invented by Henry Dudeney.^[1][2] Richard Guy and Cedric Smith were first to completely analyze the normal-play version, using Sprague-Grundy theory.^[3][4] The misère version was analyzed by William Sibert in 1973, but he did not publish his work until 1989.^[5]

The name "Kayles" is an Anglicization of the French quilles, meaning "bowling".

Analysis

Most players quickly discover that the first player has a guaranteed win in normal Kayles whenever the row length is greater than zero. This win can be achieved using a symmetry strategy. On his or her first move, the first player should move so that the row is broken into two sections of equal length. This restricts all future moves to one section or the other. Now, the first player merely imitates the second player's moves in the opposite row.

It is more interesting to ask what the nim-value is of a row of length . This is often denoted 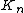; it is a nimber, not a number. By the Sprague–Grundy theorem, 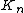is the mex over all possible moves of the nim-sum of the nim-values of the two resulting sections. For example,

because from a row of length 5, one can move to the positions

Recursive calculation of values (starting with 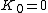) gives the results summarized in the following table. To find the value of 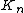on the table, write as 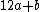, and look at row a, column b:

Kayles nim-values through

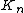	0	1	2	3	4	5	6	7	8	9	10	11
0+	0	1	2	3	1	4	3	2	1	4	2	6
12+	4	1	2	7	1	4	3	2	1	4	6	7
24+	4	1	2	8	5	4	7	2	1	8	6	7
36+	4	1	2	3	1	4	7	2	1	8	2	7
48+	4	1	2	8	1	4	7	2	1	4	2	7
60+	4	1	2	8	1	4	7	2	1	8	6	7
72+	4	1	2	8	1	4	7	2	1	8	2	7

At this point, the nim-value sequence becomes periodic^[5] with period 12, so all further rows of the table are identical to the last row.

Applications

Because certain positions in Dots and Boxes reduce to Kayles positions,^[6] it is helpful to understand Kayles in order to analyze a generic Dots and Boxes position.

Computational complexity

Under normal play, Kayles can be solved in polynomial time using the Sprague-Grundy theory.^[3]

Node Kayles is a generalization of Kayles to graphs in which each bowl “knocks down” (removes) a desired vertex and all its neighboring vertices. (Alternatively, this game can be viewed as two players finding an independent set together.) Schaefer (1978)^[7] proved that deciding the outcome of this game is PSPACE-complete. The same result holds for a partisan version of node Kayles, in which, for every node, only one of the players is allowed to choose that particular node as the knock down target.

See also

• Combinatorial game theory
• Octal games
• Dawson's Kayles
• Nimber

References

• Abasfalva
• Abasgoi
• Abash
• Abasha (disambiguation)
• Abasha District
• Abashan
• Aba Shanti-I
• Aba Shanti I
• Aba shanti-I
• Abasha (river)
• Abasha river
• Abashenko
• Abashev
• Abasheva
• Abashevo, Penza Oblast
• Abashev, Vladimir
• A Bashful Bigamist
• Abashichev
• Abashicheva
• Abashidze, Aslan
• Abashidze, Leila
• Abashidze, Nunu
• Abashin
• Abashina
• Abashiri District, Hokkaidō