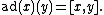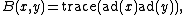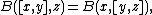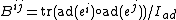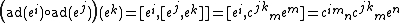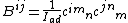“Killing form”的意思、由来-开放百科全书

词条

Killing form

释义

History and name
Definition
Properties
Matrix elements
Connection with real forms
See also
Notes
References

In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras.

History and name

The Killing form was essentially introduced into Lie algebra theory by {{harvs|txt |author-link=Élie Cartan |first=Élie |last=Cartan |year=1894}} in his thesis. The name "Killing form" first appeared in a paper of Armand Borel in 1951, but he stated in 2001 that he doesn't remember why he chose it. Borel admits that the name seems to be a misnomer, and that it would be more correct to call it the "Cartan form".^[1] Wilhelm Killing had noted that the coefficients of the characteristic equation of a regular semisimple element of a Lie algebra is invariant under the adjoint group, from which it follows that the Killing form (i.e. the degree 2 coefficient) is invariant, but he did not make much use of this fact. A basic result Cartan made use of was Cartan's criterion, which states that the Killing form is non-degenerate if and only if the Lie algebra is a direct sum of simple Lie algebras.^[1]

Definition

Consider a Lie algebra {{math|g}} over a field {{math|K}}. Every element {{math|x}} of {{math|g}} defines the adjoint endomorphism {{math|ad(x)}} (also written as {{math|ad_x}}) of {{math|g}} with the help of the Lie bracket, as

Now, supposing {{math|g}} is of finite dimension, the trace of the composition of two such endomorphisms defines a symmetric bilinear form

with values in {{math|K}}, the Killing form on {{math|g}}.

Properties

The Killing form {{math|B}} is bilinear and symmetric.
The Killing form is an invariant form, in the sense that it has the 'associativity' property

where [ , ] is the Lie bracket.

If {{math|g}} is a simple Lie algebra then any invariant symmetric bilinear form on {{math|g}} is a scalar multiple of the Killing form.
The Killing form is also invariant under automorphisms {{math|s}} of the algebra {{math|g}}, that is,

for {{math|s}} in {{math|Aut(g)}}.

The Cartan criterion states that a Lie algebra is semisimple if and only if the Killing form is non-degenerate.
The Killing form of a nilpotent Lie algebra is identically zero.
If {{math|I, J}} are two ideals in a Lie algebra {{math|g}} with zero intersection, then {{math|I}} and {{math|J}} are orthogonal subspaces with respect to the Killing form.
The orthogonal complement with respect to {{math|B}} of an ideal is again an ideal.^[2]
If a given Lie algebra {{math|g}} is a direct sum of its ideals {{math|I₁,...,I_n}}, then the Killing form of {{math|g}} is the direct sum of the Killing forms of the individual summands.

Matrix elements

Given a basis {{math|eⁱ}} of the Lie algebra {{math|g}}, the matrix elements of the Killing form are given by

where {{math|I_ad}} is the Dynkin index of the adjoint representation of {{math|g}}. Here

in Einstein summation notation, where the {{math|c^ij_k}} are the structure coefficients of the Lie algebra. The index {{math|k}} functions as column index and the index {{math|n}} as row index in the matrix {{math|ad(e_i)ad(e_j)}}. Taking the trace amounts to putting {{math|k {{=}} n}} and summing, and so we can write

The Killing form is the simplest 2-tensor that can be formed from the structure constants.

In the above indexed definition, we are careful to distinguish upper and lower indices (co- and contra-variant indices). This is because, in many cases, the Killing form can be used as a metric tensor on a manifold, in which case the distinction becomes an important one for the transformation properties of tensors. When the Lie algebra is semisimple over a zero-characteristic field, its Killing form is nondegenerate, and hence can be used as a metric tensor to raise and lower indexes. In this case, it is always possible to choose a basis for {{math|g}} such that the structure constants with all upper indices are completely antisymmetric.

The Killing form for some Lie algebras {{math|g}} are (for {{math|X, Y}} in {{math|g}} viewed in their fundamental n by n (2n by 2n) representations):

g	B(X, Y)
gl(n, R)}}	2n tr(XY) − 2 tr(X)tr(Y)}}
sl(n, R)}}	2n tr(XY)}}
su(n)}}	2n tr(XY)}}
so(n, R)}}	(n−2) tr(XY)}}
so(n)}}	(n−2) tr(XY)}}
sp(2n, R)}}	(2n+2) tr(XY)}}
sp(2n, C)}}	(2n+2) tr(XY)}}

Connection with real forms

Suppose that is a semisimple Lie algebra over the field of real numbers . By Cartan's criterion, the Killing form is nondegenerate, and can be diagonalized in a suitable basis with the diagonal entries {{math|±1}}. By Sylvester's law of inertia, the number of positive entries is an invariant of the bilinear form, i.e. it does not depend on the choice of the diagonalizing basis, and is called the index of the Lie algebra . This is a number between {{math|0}} and the dimension of which is an important invariant of the real Lie algebra. In particular, a real Lie algebra is called compact if the Killing form is negative definite (or negative semidefinite if the Lie algebra is not semisimple). Note that this is one of two inequivalent definitions commonly used for compactness of a Lie algebra; the other states that a Lie algebra is compact if it corresponds to a compact Lie group. The definition of compactness in terms of negative definiteness of the Killing form is more restrictive, since using this definition it can be shown that under the Lie correspondence, compact Lie algebras correspond to compact Lie groups.

If 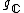is a semisimple Lie algebra over the complex numbers, then there are several non-isomorphic real Lie algebras whose complexification is , which are called its real forms. It turns out that every complex semisimple Lie algebra admits a unique (up to isomorphism) compact real form . The real forms of a given complex semisimple Lie algebra are frequently labeled by the positive index of inertia of their Killing form.

For example, the complex special linear algebra 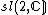has two real forms, the real special linear algebra, denoted 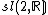, and the special unitary algebra, denoted 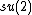. The first one is noncompact, the so-called split real form, and its Killing form has signature {{math|(2, 1)}}. The second one is the compact real form and its Killing form is negative definite, i.e. has signature {{math|(0, 3)}}. The corresponding Lie groups are the noncompact group 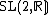of {{math|2 × 2}} real matrices with the unit determinant and the special unitary group 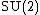, which is compact.

Notes

1. ^¹Borel, p.5
2. ^{{Fulton-Harris}} See page 207.

References

{{cite book|last1=Borel|first1=Armand|title=Essays in the history of Lie groups and algebraic groups|date=2001|publisher=American Mathematical Society and the London Mathematical Society|volume=History of Mathematics, Vol 21}}
Daniel Bump, Lie Groups (2004), Graduate Texts In Mathematics, 225, Springer-Verlag. {{isbn|978-0-387-21154-1}} {{doi|10.1007/978-1-4614-8024-2}}
{{Citation | last1=Cartan | first1=Élie | title=Sur la structure des groupes de transformations finis et continus | url=https://books.google.com/books?id=JY8LAAAAYAAJ | publisher=Nony | series=Thesis | year=1894}}
Jurgen Fuchs, Affine Lie Algebras and Quantum Groups, (1992) Cambridge University Press. {{isbn|0-521-48412-X}}
{{Fulton-Harris}}
{{springer|title=Killing form|id=p/k055400}}

2 : Lie groups|Lie algebras

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。