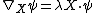- References
- Books
- External links
spinors which are also eigenspinors of the Dirac operator.[1][2][3] The term is named after Wilhelm Killing.
Another equivalent definition is that Killing spinors are the solutions to the Killing equation for a so-called Killing number.
More formally:[4]
A Killing spinor on a Riemannian spin manifold M is a spinor fieldwhich satisfies
for all tangent vectors X, whereis the spinor covariant derivative,
is Clifford multiplication and
is a constant, called the Killing number of
. If
then the spinor is called a parallel spinor.
In physics, Killing spinors are used in supergravity and superstring theory, in particular for finding solutions which preserve some supersymmetry. They are a special kind of spinor field related to Killing vector fields and Killing tensors.
References
1. ^{{cite journal|title=Der erste Eigenwert des Dirac Operators einer kompakten, Riemannschen Mannigfaltigkeit nichtnegativer Skalarkrümmung|author=Th. Friedrich|journal=Mathematische Nachrichten|volume=97|year=1980|pages=117–146|doi=10.1002/mana.19800970111}}
2. ^{{cite journal|title=On the conformal relation between twistors and Killing spinors|author=Th. Friedrich|journal=Supplemento dei Rendiconti del Circolo Matematico di Palermo, serie II|volume=22|year=1989|pages=59–75}}
3. ^{{cite journal|title=Spin manifolds, Killing spinors and the universality of Hijazi inequality|author=A. Lichnerowicz|journal=Lett. Math. Phys.|volume=13|year=1987|pages=331–334|doi=10.1007/bf00401162|bibcode = 1987LMaPh..13..331L }}
4. ^{{citation | last1=Friedrich|first1=Thomas| title = Dirac Operators in Riemannian Geometry| publisher=American Mathematical Society |pages= 116–117| year=2000|isbn=978-0-8218-2055-1}}
2. ^{{cite journal|title=On the conformal relation between twistors and Killing spinors|author=Th. Friedrich|journal=Supplemento dei Rendiconti del Circolo Matematico di Palermo, serie II|volume=22|year=1989|pages=59–75}}
3. ^{{cite journal|title=Spin manifolds, Killing spinors and the universality of Hijazi inequality|author=A. Lichnerowicz|journal=Lett. Math. Phys.|volume=13|year=1987|pages=331–334|doi=10.1007/bf00401162|bibcode = 1987LMaPh..13..331L }}
4. ^{{citation | last1=Friedrich|first1=Thomas| title = Dirac Operators in Riemannian Geometry| publisher=American Mathematical Society |pages= 116–117| year=2000|isbn=978-0-8218-2055-1}}
Books
- {{Cite book | last1=Lawson | first1=H. Blaine | last2=Michelsohn | first2=Marie-Louise |author2-link=Marie-Louise Michelsohn| title=Spin Geometry | publisher=Princeton University Press | isbn=978-0-691-08542-5 | year=1989 | postscript=}}
- {{citation | last1=Friedrich|first1=Thomas| title = Dirac Operators in Riemannian Geometry| publisher=American Mathematical Society | year=2000|isbn=978-0-8218-2055-1}}
External links
- "Twistor and Killing spinors in Lorentzian geometry," by Helga Baum (PDF format)
- Dirac Operator From MathWorld
- Killing's Equation From MathWorld
- [https://web.archive.org/web/20041107222740/http://www.math.tu-berlin.de/~bohle/pub/dipl.ps Killing and Twistor Spinors on Lorentzian Manifolds, (paper by Christoph Bohle) (postscript format) ]
4 : Riemannian geometry|Structures on manifolds|Supersymmetry|Spinors
- Single current systems
- Single-current systems
- Single current transmission system
- Singlecurrent transmission systems
- Single-current transmission systems
- Single current transmission systems
- Single cycle processor
- Single Dad in Love
- Single dealer platform
- Single-dealer platform
- Single-deck bus
- Single-decker
- Single decker
- Single decker bus
- Single-decker bus
- Single decker buses
- Single-decker buses
- Single deckers
- Single-deckers
- Single-density
- Single deposit
- Singledestination shortestpath problem
- Single destination shortestpath problem
- Single-destination shortestpath problem
- Single destination shortest path problem