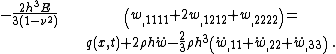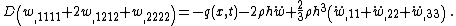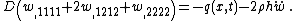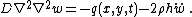- Assumed displacement field
- Quasistatic Kirchhoff-Love plates Strain-displacement relations Equilibrium equations Boundary conditions Constitutive relations Small strains and moderate rotations
- Isotropic quasistatic Kirchhoff-Love plates Pure bending Bending under transverse load Cylindrical bending
- Dynamics of Kirchhoff-Love plates Governing equations Isotropic plates
- References
- See also
The Kirchhoff–Love theory of plates is a two-dimensional mathematical model that is used to determine the stresses and deformations in thin plates subjected to forces and moments. This theory is an extension of Euler-Bernoulli beam theory and was developed in 1888 by Love[1] using assumptions proposed by Kirchhoff. The theory assumes that a mid-surface plane can be used to represent a three-dimensional plate in two-dimensional form.
The following kinematic assumptions that are made in this theory:[2]
- straight lines normal to the mid-surface remain straight after deformation
- straight lines normal to the mid-surface remain normal to the mid-surface after deformation
- the thickness of the plate does not change during a deformation.
Assumed displacement field
Let the position vector of a point in the undeformed plate be  . Then
. Then
The vectors 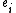 form a Cartesian basis with origin on the mid-surface of the plate,
form a Cartesian basis with origin on the mid-surface of the plate, 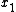 and
and 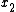 are the Cartesian coordinates on the mid-surface of the undeformed plate, and
are the Cartesian coordinates on the mid-surface of the undeformed plate, and 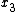 is the coordinate for the thickness direction.
is the coordinate for the thickness direction.
Let the displacement of a point in the plate be 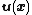 . Then
. Then
This displacement can be decomposed into a vector sum of the mid-surface displacement 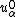 and an out-of-plane displacement
and an out-of-plane displacement 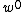 in the
in the 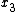 direction. We can write the in-plane displacement of the mid-surface as
direction. We can write the in-plane displacement of the mid-surface as
Note that the index  takes the values 1 and 2 but not 3.
takes the values 1 and 2 but not 3.
Then the Kirchhoff hypothesis implies that
{{Equation box 1|indent=:|equation=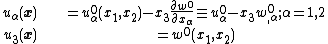
|border colour=#50C878 |background colour = #ECFCF4}}
If 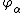 are the angles of rotation of the normal to the mid-surface, then in the Kirchhoff-Love theory
are the angles of rotation of the normal to the mid-surface, then in the Kirchhoff-Love theory
Note that we can think of the expression for 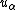 as the first order Taylor series expansion of the displacement around the mid-surface.
as the first order Taylor series expansion of the displacement around the mid-surface.
Quasistatic Kirchhoff-Love plates
The original theory developed by Love was valid for infinitesimal strains and rotations. The theory was extended by von Kármán to situations where moderate rotations could be expected.
Strain-displacement relations
For the situation where the strains in the plate are infinitesimal and the rotations of the mid-surface normals are less than 10° the strain-displacement relations are
where 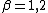 as
as  .
.
Using the kinematic assumptions we have
{{Equation box 1 |indent =:| equation=
|border colour=#50C878 |background colour = #ECFCF4}}
Therefore, the only non-zero strains are in the in-plane directions.
Equilibrium equations
The equilibrium equations for the plate can be derived from the principle of virtual work. For a thin plate under a quasistatic transverse load 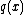 these equations are
these equations are
where the thickness of the plate is 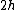 . In index notation,
. In index notation,
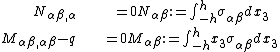
|border colour=#50C878 |background colour = #ECFCF4}}
where 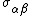 are the stresses.
are the stresses.
| Derivation of equilibrium equations for small rotations |
|---|
| For the situation where the strains and rotations of the plate are small the virtual internal energy is given by where the thickness of the plate is Integration by parts leads to The symmetry of the stress tensor implies that Another integration by parts gives For the case where there are no prescribed external forces, the principle of virtual work implies that If the plate is loaded by an external distributed load The principle of virtual work then leads to the equilibrium equations |
Boundary conditions
The boundary conditions that are needed to solve the equilibrium equations of plate theory can be obtained from the boundary terms in the principle of virtual work. In the absence of external forces on the boundary, the boundary conditions are
Note that the quantity 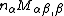 is an effective shear force.
is an effective shear force.
Constitutive relations
The stress-strain relations for a linear elastic Kirchhoff plate are given by
Since 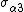 and
and 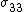 do not appear in the equilibrium equations it is implicitly assumed that these quantities do not have any effect on the momentum balance and are neglected. The remaining stress-strain relations, in matrix form, can be written as
do not appear in the equilibrium equations it is implicitly assumed that these quantities do not have any effect on the momentum balance and are neglected. The remaining stress-strain relations, in matrix form, can be written as
Then,
and
The extensional stiffnesses are the quantities
The bending stiffnesses (also called flexural rigidity) are the quantities
The Kirchhoff-Love constitutive assumptions lead to zero shear forces. As a result, the equilibrium equations for the plate have to be used to determine the shear forces in thin Kirchhoff-Love plates. For isotropic plates, these equations lead to
Alternatively, these shear forces can be expressed as
where
Small strains and moderate rotations
If the rotations of the normals to the mid-surface are in the range of 10 to 15
to 15 , the strain-displacement relations can be approximated as
, the strain-displacement relations can be approximated as
Then the kinematic assumptions of Kirchhoff-Love theory lead to the classical plate theory with von Kármán strains
This theory is nonlinear because of the quadratic terms in the strain-displacement relations.
If the strain-displacement relations take the von Karman form, the equilibrium equations can be expressed as
Isotropic quasistatic Kirchhoff-Love plates
For an isotropic and homogeneous plate, the stress-strain relations are
where  is Poisson's Ratio and
is Poisson's Ratio and  is Young's Modulus. The moments corresponding to these stresses are
is Young's Modulus. The moments corresponding to these stresses are
In expanded form,
where 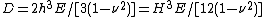 for plates of thickness
for plates of thickness 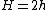 . Using the stress-strain relations for the plates, we can show that the stresses and moments are related by
. Using the stress-strain relations for the plates, we can show that the stresses and moments are related by
At the top of the plate where 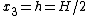 , the stresses are
, the stresses are
Pure bending
For an isotropic and homogeneous plate under pure bending, the governing equations reduce to
Here we have assumed that the in-plane displacements do not vary with 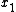 and
and 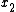 . In index notation,
. In index notation,
and in direct notation
{{Equation box 1 |indent =:| equation=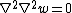
|border colour=#50C878 |background colour = #ECFCF4}}
The bending moments are given by
| Derivation of equilibrium equations for pure bending |
|---|
| For an isotropic, homogeneous plate under pure bending the governing equations are and the stress-strain relations are Then, and Differentiation gives and Plugging into the governing equations leads to Since the order of differentiation is irrelevant we have In direct tensor notation, the governing equation of the plate is where we have assumed that the displacements |
Bending under transverse load
If a distributed transverse load 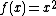 is applied to the plate, the governing equation is
is applied to the plate, the governing equation is 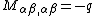 . Following the procedure shown in the previous section we get[3]
. Following the procedure shown in the previous section we get[3]
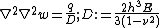
|border colour=#50C878 |background colour = #ECFCF4}}
In rectangular Cartesian coordinates, the governing equation is
and in cylindrical coordinates it takes the form
Solutions of this equation for various geometries and boundary conditions can be found in the article on bending of plates.
| Derivation of equilibrium equations for transverse loading | |
|---|---|
| For a transversely loaded plate without axial deformations, the governing equation has the form where Noting that the bending stiffness is the quantity we can write the governing equation in the form {{Equation box 1 |indent =:| equation=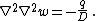 | background colour = #ECFCF4} In cylindrical coordinates For symmetrically loaded circular plates, |
Cylindrical bending
Under certain loading conditions a flat plate can be bent into the shape of the surface of a cylinder. This type of bending is called cylindrical bending and represents the special situation where 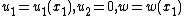 . In that case
. In that case
and
and the governing equations become[3]
Dynamics of Kirchhoff-Love plates
The dynamic theory of thin plates determines the propagation of waves in the plates, and the study of standing waves and vibration modes.
Governing equations
The governing equations for the dynamics of a Kirchhoff-Love plate are
{{Equation box 1 |indent =:| equation=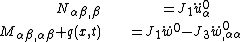
|border colour=#50C878 |background colour = #ECFCF4}}
where, for a plate with density 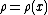 ,
,
and
| Derivation of equations governing the dynamics of Kirchhoff-Love plates |
|---|
Solutions of these equations for some special cases can be found in the article on vibrations of plates. The figures below show some vibrational modes of a circular plate.
Isotropic plates
The governing equations simplify considerably for isotropic and homogeneous plates for which the in-plane deformations can be neglected. In that case we are left with one equation of the following form (in rectangular Cartesian coordinates):
where  is the bending stiffness of the plate. For a uniform plate of thickness
is the bending stiffness of the plate. For a uniform plate of thickness 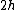 ,
,
In direct notation
For free vibrations, the governing equation becomes
| Derivation of dynamic governing equations for isotropic Kirchhoff-Love plates |
|---|
References
2. ^Reddy, J. N., 2007, Theory and analysis of elastic plates and shells, CRC Press, Taylor and Francis.
3. ^1 Timoshenko, S. and Woinowsky-Krieger, S., (1959), Theory of plates and shells, McGraw-Hill New York.
See also
- Bending
- Bending of plates
- Infinitesimal strain theory
- Linear elasticity
- Plate theory
- Stress (mechanics)
- Stress resultants
- Vibration of plates
- Anglo Platinum
- Anglo-Polish Agreement of Mutual Assistance
- Anglo-Portuguese Army
- Anglo-Portuguese relations
- Anglo-Portuguese Treaty of 1891
- Anglo-Prussian Alliance
- Anglo-Prussian alliance (1788)
- Anglo-Prussian alliance (disambiguation)
- Anglo-Quebeckers
- Anglo-Russian
- Anglo-Russian Agreement over Constantinople
- Anglo-Russian Hospital
- Anglo-Russian Invasion of Holland
- Anglo-Russians
- Anglo-Saxon Amulets and Curing Stones
- Anglo-Saxon Clubs of America
- Anglo-Saxon coinage
- Anglo-Saxon Cotton world map
- Anglo-Saxon cross
- Anglo-Saxon deities
- Anglo-Saxon Deviant Burial Customs
- Anglo-Saxon economy
- Anglo-Saxon genealogies
- Anglo-Saxon Genealogies
- Anglo-Saxon Herefordshire
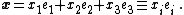
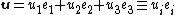
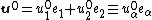
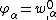
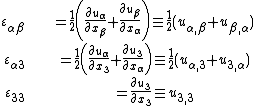
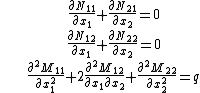
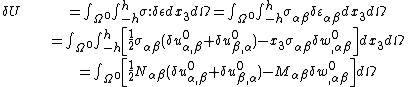
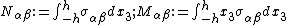
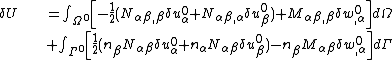
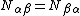 . Hence,
. Hence,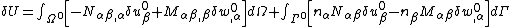
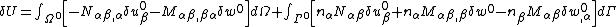
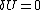 . The equilibrium equations for the plate are then given by
. The equilibrium equations for the plate are then given by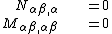
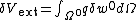
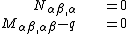
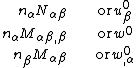
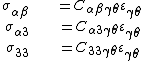
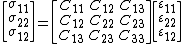
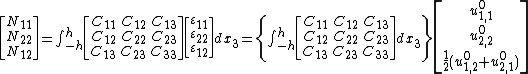

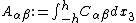
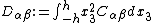
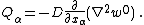
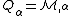
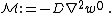
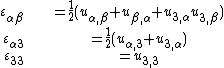
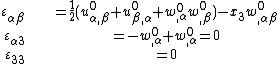
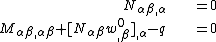
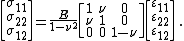
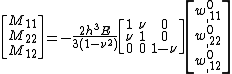



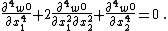
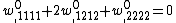
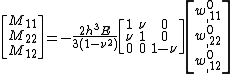
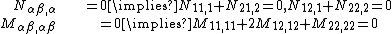
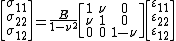
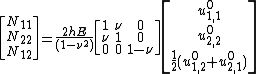
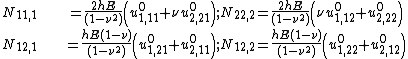
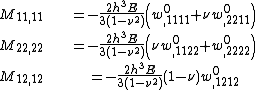

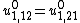 ,
, 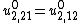 , and
, and 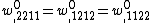 . Hence
. Hence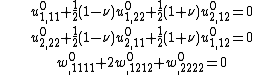
 are constant.
are constant.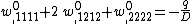
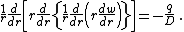
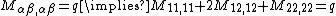
 is a distributed transverse load (per unit area). Substitution of the expressions for the derivatives of
is a distributed transverse load (per unit area). Substitution of the expressions for the derivatives of 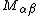 into the governing equation gives
into the governing equation gives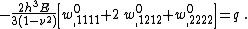
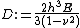
 ,
,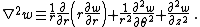
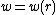 , and we have
, and we have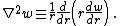
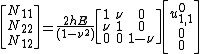
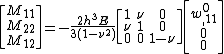
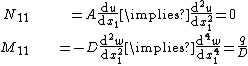
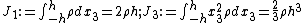
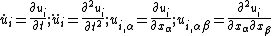
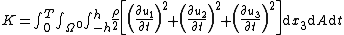
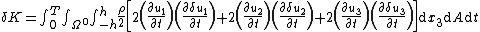
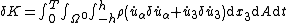
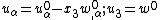
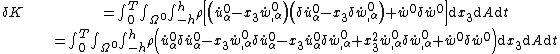
 through the thickness of the plate,
through the thickness of the plate,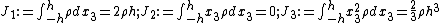
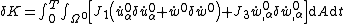
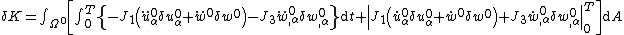
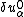 and
and 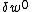 are zero at
are zero at 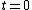 and
and 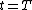 .
.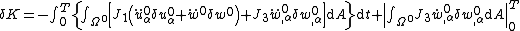
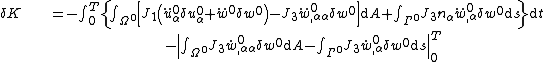
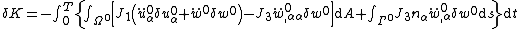

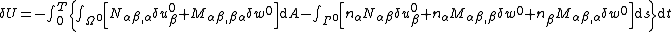
 acting normal to the surface of the plate, the virtual external work done is
acting normal to the surface of the plate, the virtual external work done is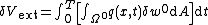
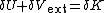 . Hence the governing balance equations for the plate are
. Hence the governing balance equations for the plate are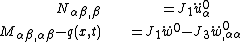
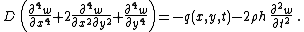

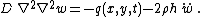
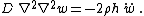
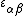 are the in-plane strains. The strain-displacement relations
are the in-plane strains. The strain-displacement relations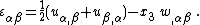
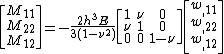
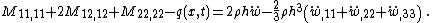
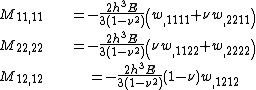
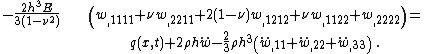
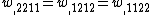 . Hence
. Hence