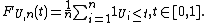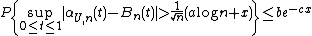“Komlós–Major–Tusnády approximation”的意思、由来-开放百科全书

词条

Komlós–Major–Tusnády approximation

释义

Theory
Corollary
References

In theory of probability, the Komlós–Major–Tusnády approximation (also known as the KMT approximation, the KMT embedding, or the Hungarian embedding) is an approximation of the empirical process by a Gaussian process constructed on the same probability space. It is named after Hungarian mathematicians János Komlós, Gábor Tusnády, and Péter Major.

Theory

Let be independent uniform (0,1) random variables. Define a uniform empirical distribution function as

Define a uniform empirical process as

The Donsker theorem (1952) shows that 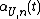converges in law to a Brownian bridge Komlós, Major and Tusnády established a sharp bound for the speed of this weak convergence.

Theorem (KMT, 1975) On a suitable probability space for independent uniform (0,1) r.v. the empirical process can be approximated by a sequence of Brownian bridges such that

for all positive integers n and all , where a, b, and c are positive constants.

Corollary

A corollary of that theorem is that for any real iid r.v. 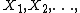with cdf 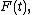it is possible to construct a probability space where independent{{Clarify|reason=surely alpha and B can't be independent, so what is independent of what?|date=January 2012}} sequences of empirical processes 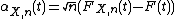and Gaussian processes 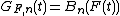exist such that

almost surely.

References

Komlos, J., Major, P. and Tusnady, G. (1975) An approximation of partial sums of independent rv’s and the sample df. I, Wahrsch verw Gebiete/Probability Theory and Related Fields, 32, 111–131. {{DOI| 10.1007/BF00533093}}
Komlos, J., Major, P. and Tusnady, G. (1976) An approximation of partial sums of independent rv’s and the sample df. II, Wahrsch verw Gebiete/Probability Theory and Related Fields, 34, 33–58. {{doi|10.1007/BF00532688 }}

1 : Empirical process

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。