“Kirszbraun theorem”的意思、由来-开放百科全书

In mathematics, specifically real analysis and functional analysis, the Kirszbraun theorem states that if U is a subset of some Hilbert space H₁, and H₂ is another Hilbert space, and

Note that this result in particular applies to Euclidean spaces Eⁿ and E^m, and it was in this form that Kirszbraun originally formulated and proved the theorem.^[1] The version for Hilbert spaces can for example be found in (Schwartz 1969, p. 21).^[2] If H₁ is a separable space (in particular, if it is a Euclidean space) the result is true in Zermelo–Fraenkel set theory; for the fully general case, it appears to need some form of the axiom of choice; the Boolean prime ideal theorem is known to be sufficient.^[3]

The proof of the theorem uses geometric features of Hilbert spaces; the corresponding statement for Banach spaces is not true in general, not even for finite-dimensional Banach spaces. It is for instance possible to construct counterexamples where the domain is a subset of Rⁿ with the maximum norm and R^m carries the Euclidean norm.^[4] More generally, the theorem fails for

equipped with any

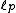norm (

) (Schwartz 1969, p. 20).^[2]

For an R-valued function the extension is provided by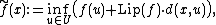

where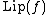

is f's Lipschitz constant on U.

History

The theorem was proved by Mojżesz David Kirszbraun, and later it was reproved by Frederick Valentine,^[5] who first proved it for the Euclidean plane.^[6] Sometimes this theorem is also called Kirszbraun–Valentine theorem.

References

1. ^{{cite journal |first=M. D. |last=Kirszbraun |title=Über die zusammenziehende und Lipschitzsche Transformationen |journal=Fund. Math. |volume=22 |issue= |pages=77–108 |year=1934 |doi= }}
2. ^¹{{cite book |authorlink=Jack Schwartz |first=J. T. |last=Schwartz |title=Nonlinear functional analysis |publisher=Gordon and Breach Science |location=New York |year=1969 }}
3. ^{{cite paper |first=D. H. |last=Fremlin |year=2011 |title=Kirszbraun's theorem |work=Preprint |url=http://www.essex.ac.uk/maths/people/fremlin/n11706.pdf }}
4. ^{{cite book |first=H. |last=Federer |title=Geometric Measure Theory |publisher=Springer |location=Berlin |year=1969 |page=202 |isbn= }}
5. ^{{cite journal |first=F. A. |last=Valentine |title=A Lipschitz Condition Preserving Extension for a Vector Function |journal=American Journal of Mathematics |volume=67 |issue=1 |year=1945 |pages=83–93 |doi=10.2307/2371917 }}
6. ^{{cite journal |first=F. A. |last=Valentine |title=On the extension of a vector function so as to preserve a Lipschitz condition |journal=Bulletin of the American Mathematical Society |volume=49 |issue= |pages=100–108 |year=1943 |mr=0008251 |doi=10.1090/s0002-9904-1943-07859-7}}

History

References

External links