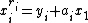“Krull's principal ideal theorem”的意思、由来-开放百科全书

词条

Krull's principal ideal theorem

释义

Proofs
Proof of the principal ideal theorem Proof of the height theorem
References

In commutative algebra, Krull's principal ideal theorem, named after Wolfgang Krull (1899–1971), gives a bound on the height of a principal ideal in a commutative Noetherian ring. The theorem is sometimes referred to by its German name, Krulls Hauptidealsatz (Satz meaning "proposition" or "theorem").

Formally, if R is a Noetherian ring and I is a principal, proper ideal of R, then I has height at most one.

This theorem can be generalized to ideals that are not principal, and the result is often called Krull's height theorem. This says that if R is a Noetherian ring and I is a proper ideal generated by n elements of R, then I has height at most n.

The principal ideal theorem and the generalization, the height theorem, both follow from the fundamental theorem of dimension theory in commutative algebra (see also below for the direct proofs). Bourbaki's Commutative Algebra gives a direct proof. Kaplansky's Commutative ring includes a proof due to David Rees.

Proofs

Proof of the principal ideal theorem

Let be a Noetherian ring, x an element of it and a minimal prime over x. Replacing A by the localization , we can assume is local with the maximal ideal . Let be a strictly smaller prime ideal and let , which is a -primary ideal called the n-th symbolic power of . It forms a descending chain of ideals 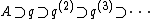. Thus, there is the descending chain of ideals in the ring . Now, the radical is the intersection of all minimal prime ideals containg ; is among them. But is a unique maximal ideal and thus . Since 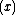contains some power of its radical, it follows that is an Artinian ring and thus the chain stabilizes and so there is some n such that . It implies:

,

from the fact is -primary (if is in , then with and . Since is minimal over , and so implies is in .) Then, by Nakayama's lemma, and thus . Using Nakayama's lemma again, 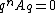and is an Artinian ring; thus, the height of is zero.

Proof of the height theorem

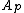Krull’s height theorem can be proved as a consequence of the principal ideal theorem by induction on the number of elements. Let be elements in , a minimal prime over and a prime ideal such that there is no prime strictly between them. Replacing by the localization we can assume 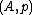is a local ring; note we then have . By minimality, cannot contain all the ; relabeling the subscripts, say, 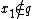. Since every prime ideal containing is between and , 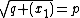and thus we can write for each ,

with 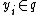and . Now we consider the ring and the corresponding chain in it. If is a minimal prime over , then contains and thus ; that is to say, is a minimal prime over and so, by Krull’s principal ideal theorem, is a minimal prime (over zero); is a minimal prime over . By inductive hypothesis, and thus .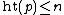

References

{{Citation | last1=Matsumura | first1=Hideyuki | title=Commutative Algebra | publisher=Benjamin | location=New York | year=1970}}, see in particular section (12.I), p. 77
http://www.math.lsa.umich.edu/~hochster/615W10/supDim.pdf

3 : Commutative algebra|Ideals|Theorems in abstract algebra

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。