请输入您要查询的百科知识：

　

词条 Kruskal's algorithm
释义

  1. Algorithm

  2. Pseudocode

  3. Complexity

  4. Example

  5. Proof of correctness

     Spanning tree  Minimality 

  6. Parallel Algorithm

  7. See also

  8. References

  9. External links

{{More citations needed|date=September 2018}}{{graph search algorithm}}

Kruskal's algorithm is a minimum-spanning-tree algorithm which finds an edge of the least possible weight that connects any two trees in the forest.[1] It is a greedy algorithm in graph theory as it finds a minimum spanning tree for a connected weighted graph adding increasing cost arcs at each step.[1] This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component).

This algorithm first appeared in Proceedings of the American Mathematical Society, pp. 48–50 in 1956, and was written by Joseph Kruskal.[2]

Other algorithms for this problem include Prim's algorithm, Reverse-delete algorithm, and Borůvka's algorithm.

Algorithm

  • create a forest F (a set of trees), where each vertex in the graph is a separate tree
  • create a set S containing all the edges in the graph
  • while S is nonempty and F is not yet spanning
    • remove an edge with minimum weight from S
    • if the removed edge connects two different trees then add it to the forest F, combining two trees into a single tree

At the termination of the algorithm, the forest forms a minimum spanning forest of the graph. If the graph is connected, the forest has a single component and forms a minimum spanning tree

Pseudocode

The following code is implemented with disjoint-set data structure:

 KRUSKAL(G): 1 A = ∅ 2 '''foreach''' v ∈ G.V: 3    MAKE-SET(v) 4 '''foreach''' (u, v) in G.E ordered by weight(u, v), increasing: 5    '''if''' FIND-SET(u) ≠ FIND-SET(v): 6       A = A ∪ {(u, v)} 7       UNION(u, v) 8 '''return''' A

Complexity

Kruskal's algorithm can be shown to run in O(E log E) time, or equivalently, O(E log V) time, where E is the number of edges in the graph and V is the number of vertices, all with simple data structures. These running times are equivalent because:

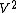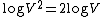  • E is at most and is .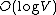
  • Each isolated vertex is a separate component of the minimum spanning forest. If we ignore isolated vertices we obtain V ≤ 2E, so log V is .

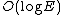We can achieve this bound as follows: first sort the edges by weight using a comparison sort in O(E log E) time; this allows the step "remove an edge with minimum weight from S" to operate in constant time. Next, we use a disjoint-set data structure to keep track of which vertices are in which components. We need to perform O(V) operations, as in each iteration we connect a vertex to the spanning tree, two 'find' operations and possibly one union for each edge. Even a simple disjoint-set data structure such as disjoint-set forests with union by rank can perform O(V) operations in O(V log V) time. Thus the total time is O(E log E) = O(E log V).

Provided that the edges are either already sorted or can be sorted in linear time (for example with counting sort or radix sort), the algorithm can use a more sophisticated disjoint-set data structure to run in O(E α(V)) time, where α is the extremely slowly growing inverse of the single-valued Ackermann function.

Example

Image Description
AD and CE are the shortest edges, with length 5, and AD has been arbitrarily chosen, so it is highlighted.
CE is now the shortest edge that does not form a cycle, with length 5, so it is highlighted as the second edge.
The next edge, DF with length 6, is highlighted using much the same method.
The next-shortest edges are AB and BE, both with length 7. AB is chosen arbitrarily, and is highlighted. The edge BD has been highlighted in red, because there already exists a path (in green) between B and D, so it would form a cycle (ABD) if it were chosen.
The process continues to highlight the next-smallest edge, BE with length 7. Many more edges are highlighted in red at this stage: BC because it would form the loop BCE, DE because it would form the loop DEBA, and FE because it would form FEBAD.
Finally, the process finishes with the edge EG of length 9, and the minimum spanning tree is found.

Proof of correctness

The proof consists of two parts. First, it is proved that the algorithm produces a spanning tree. Second, it is proved that the constructed spanning tree is of minimal weight.

Spanning tree

Let be a connected, weighted graph and let be the subgraph of produced by the algorithm. cannot have a cycle, being within one subtree and not between two different trees. cannot be disconnected, since the first encountered edge that joins two components of would have been added by the algorithm. Thus, is a spanning tree of .

Minimality

We show that the following proposition P is true by induction: If F is the set of edges chosen at any stage of the algorithm, then there is some minimum spanning tree that contains F.

  • Clearly P is true at the beginning, when F is empty: any minimum spanning tree will do, and there exists one because a weighted connected graph always has a minimum spanning tree.
  • Now assume P is true for some non-final edge set F and let T be a minimum spanning tree that contains F.
    • If the next chosen edge e is also in T, then P is true for F + e.
    • Otherwise, e is not in T, and T + e has a cycle C. This cycle contains edges which do not belong to F, since e does not form a cycle in F but does in T. Let f be an edge in C but not in F. Note that f belongs also to T, and by P has not be considered by the algorithm, and hence a weight at least as large as e. Then T − f + e is a tree, and it has the same or less weight as T. So T − f + e is a minimum spanning tree containing F + e and again P holds.
  • Therefore, by the principle of induction, P holds when F has become a spanning tree, which is only possible if F is a minimum spanning tree itself.

Parallel Algorithm

Kruskal's algorithm is inherently sequential and hard to parallelize. It is, however, possible to perform the initial sorting of the edges in parallel or, alternatively, to use a parallel implementation of a binary heap to extract the minimum-weight edge in every iteration[3].

As parallel sorting is possible in time 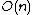on processors[4], the runtime of Kruskal's algorithm can be reduced to O(E α(V)), where α again is the inverse of the single-valued Ackermann function.

A variant of Kruskal's algorithm, named Filter-Kruskal, has been described by Osipov et al.[5] and is better suited for parallelization. The basic idea behind Filter-Kruskal is to partition the edges in a similar way to quicksort and filter out edges that connect vertices of the same tree to reduce the cost of sorting. The following Pseudocode demonstrates this.

  FILTER-KRUSKAL(G): 1 '''if''' |G.E| < KruskalThreshhold: 2    '''return''' KRUSKAL(G) 3 pivot = CHOOSE-RANDOM(G.E) 4 ,  = PARTITION(G.E, pivot) 5 A = FILTER-KRUSKAL() 6  = FILTER() 7 A = A ∪ FILTER-KRUSKAL() 8 '''return''' A  PARTITION(E, pivot): 1  = ∅,  = ∅ 2 '''foreach''' (u, v) in E: 3    '''if''' weight(u, v) <= pivot: 4        =  ∪ {(u, v)} 5    '''else''' 6        =  ∪ {(u, v)} 5 '''return''' ,   FILTER(E): 1  = ∅ 2 '''foreach''' (u, v) in E: 3    '''if''' FIND-SET(u) ≠ FIND-SET(v): 4        =  ∪ {(u, v)} 5 '''return'''

Filter-Kruskal lends itself better for parallelization as sorting, filtering, and partitioning can easily be performed in parallel by distributing the edges between the processors[5].

Finally, other variants of a parallel implementation of Kruskal's algorithm have been explored. Examples include a scheme that uses helper threads to remove edges that are definitely not part of the MST in the background[6], and a variant which runs the sequential algorithm on p subgraphs, then merges those subgraphs until only one, the final MST, remains[7].

See also

  • Dijkstra's algorithm
  • Prim's algorithm
  • Borůvka's algorithm
  • Reverse-delete algorithm
  • Single-linkage clustering
  • Greedy geometric spanner

References

1. ^1 {{Cite book|title = Introduction To Algorithms|last = Cormen|first = Thomas|publisher = MIT Press|year = 2009|isbn = 0262258102|location = |pages = 631|last2 = Charles E Leiserson, Ronald L Rivest, Clifford Stein|edition = Third}}
2. ^{{Cite journal | last1 = Kruskal | first1 = J. B. | authorlink1 = Joseph Kruskal| doi = 10.1090/S0002-9939-1956-0078686-7 | title = On the shortest spanning subtree of a graph and the traveling salesman problem | journal = Proceedings of the American Mathematical Society | volume = 7 | pages = 48–50 | year = 1956| jstor = 2033241| pmid = | pmc = }}
3. ^{{Cite journal|last1=Quinn|first1=Michael J.|last2=Deo|first2=Narsingh|date=1984|title=Parallel graph algorithms|url=|journal=ACM Computing Surveys (CSUR) 16.3|volume=|pages=319-348|via=}}
4. ^{{cite book|title=Introduction to Parallel Computing|last1=Grama|first1=Ananth|last2=Gupta|first2=Anshul|last3=Karypis|first3=George|last4=Kumar|first4=Vipin|publisher=|year=2003|isbn=978-0201648652|location=|pages=412-413}}
5. ^1 {{Cite journal|last1=Osipov|first1=Vitaly|last2=Sanders|first2=Peter|last3=Singler|first3=Johannes|date=2009|title=The filter-kruskal minimum spanning tree algorithm|url=|journal=Proceedings of the Eleventh Workshop on Algorithm Engineering and Experiments (ALENEX). Society for Industrial and Applied Mathematics|volume=|pages=52-61|via=}}
6. ^{{Cite journal|last1=Katsigiannis|first1=Anastasios|last2=Anastopoulos|first2=Nikos|last3=Konstantinos|first3=Nikas|last4=Koziris|first4=Nectarios|date=2012|title=An approach to parallelize kruskal's algorithm using helper threads|url=|journal=Parallel and Distributed Processing Symposium Workshops & PhD Forum (IPDPSW), 2012 IEEE 26th International|volume=|pages=1601-1610|via=}}
7. ^{{Cite journal|last1=Lončar|first1=Vladimir|last2=Škrbić|first2=Srdjan|last3=Balaž|first3=Antun|date=2014|title=Parallelization of Minimum Spanning Tree Algorithms Using Distributed Memory Architectures|url=|journal=Transactions on Engineering Technologies.|volume=|pages=543-554|via=}}
  • Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. {{isbn|0-262-03293-7}}. Section 23.2: The algorithms of Kruskal and Prim, pp. 567–574.
  • Michael T. Goodrich and Roberto Tamassia. Data Structures and Algorithms in Java, Fourth Edition. John Wiley & Sons, Inc., 2006. {{isbn|0-471-73884-0}}. Section 13.7.1: Kruskal's Algorithm, pp. 632..

External links

  • Kruskal's Algorithm with example and program in c++
  • [https://meyavuz.wordpress.com/2017/03/11/how-does-kruskals-algorithm-progress/ Kruskal's Algorithm code in C++ as applied to random numbers]

4 : Graph algorithms|Spanning tree|Articles with example pseudocode|Articles containing proofs
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/14 20:43:20