1. Method

2. Exact probability tables

3. Exact distribution of

4. See also

5. References

6. Further reading

7. External links

The Kruskal–Wallis test by ranks, Kruskal–Wallis H test^[1] (named after William Kruskal and W. Allen Wallis), or one-way ANOVA on ranks^[1] is a non-parametric method for testing whether samples originate from the same distribution.^[2][3][4] It is used for comparing two or more independent samples of equal or different sample sizes. It extends the Mann–Whitney U test, which is used for comparing only two groups. The parametric equivalent of the Kruskal–Wallis test is the one-way analysis of variance (ANOVA).

A significant Kruskal–Wallis test indicates that at least one sample stochastically dominates one other sample. The test does not identify where this stochastic dominance occurs or for how many pairs of groups stochastic dominance obtains. For analyzing the specific sample pairs for stochastic dominance, Dunn's test,^[5] pairwise Mann-Whitney tests without Bonferroni correction,^[6] or the more powerful but less well known Conover–Iman test^[7] are sometimes used.

Since it is a non-parametric method, the Kruskal–Wallis test does not assume a normal distribution of the residuals, unlike the analogous one-way analysis of variance. If the researcher can make the assumptions of an identically shaped and scaled distribution for all groups, except for any difference in medians, then the null hypothesis is that the medians of all groups are equal, and the alternative hypothesis is that at least one population median of one group is different from the population median of at least one other group.

Method

1. Rank all data from all groups together; i.e., rank the data from 1 to N ignoring group membership. Assign any tied values the average of the ranks they would have received had they not been tied.
2. The test statistic is given by:

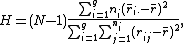   where:

   • is the number of observations in group
   • is the rank (among all observations) of observation from group
   • is the total number of observations across all groups
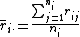   • is the average rank of all observations in group
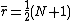   • is the average of all the .
3. If the data contain no ties the denominator of the expression for is exactly and 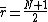. Thus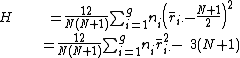

   
   The last formula only contains the squares of the average ranks.

4. A correction for ties if using the short-cut formula described in the previous point can be made by dividing by 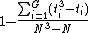, where G is the number of groupings of different tied ranks, and t_i is the number of tied values within group i that are tied at a particular value. This correction usually makes little difference in the value of H unless there are a large number of ties.
5. Finally, the decision to reject or not the null hypothesis is made by comparing to a critical value obtained from a table or a software for a given significan or alpha level. If is bigger than , the null hypothesis is rejected. If possible (no ties, sample not too big) one should compare to the critical value obtained from the exact distribution of . Otherwise, the distribution of H can be approximated by a chi-squared distribution with g-1 degrees of freedom. If some values are small (i.e., less than 5) the exact probability distribution of can be quite different from this chi-squared distribution. If a table of the chi-squared probability distribution is available, the critical value of chi-squared, 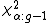, can be found by entering the table at g − 1 degrees of freedom and looking under the desired significance or alpha level.
6. If the statistic is not significant, then there is no evidence of stochastic dominance between the samples. However, if the test is significant then at least one sample stochastically dominates another sample. Therefore, a researcher might use sample contrasts between individual sample pairs, or post hoc tests using Dunn's test, which (1) properly employs the same rankings as the Kruskal–Wallis test, and (2) properly employs the pooled variance implied by the null hypothesis of the Kruskal–Wallis test in order to determine which of the sample pairs are significantly different.^&91;5&93; When performing multiple sample contrasts or tests, the Type I error rate tends to become inflated, raising concerns about multiple comparisons.

Exact probability tables

A large amount of computing resources is required to compute exact probabilities for the Kruskal–Wallis test. Existing software only provides exact probabilities for sample sizes less than about 30 participants. These software programs rely on asymptotic approximation for larger sample sizes.

Exact probability values for larger sample sizes are available. Spurrier (2003) published exact probability tables for samples as large as 45 participants.^[8] Meyer and Seaman (2006) produced exact probability distributions for samples as large as 105 participants.^[9]

Exact distribution of

Choi et al.^[10]

make a review of two methods that had been developed to compute the exact distribution of , propose a new one, and compare the exact distribution to its chi-squared approximation.

See also

• Friedman test
• Jonckheere's trend test

References

Further reading

• {{cite book |last=Daniel |first=Wayne W. |chapter=Kruskal–Wallis one-way analysis of variance by ranks |title=Applied Nonparametric Statistics |location=Boston |publisher=PWS-Kent |edition=2nd |year=1990 |isbn=0-534-91976-6 |pages=226–234 |chapterurl=https://books.google.com/books?id=0hPvAAAAMAAJ&pg=PA226 }}

External links

• An online version of the test

• Rodin Alper Bingöl
• Rodin Deprem
• Rodinei Marcelo de Almeida
• Rodin (film)
• Rodin Gallery
• Rodingite
• Rodinian
• Rodin, Kirill
• Rodin museum
• Rodinna pouta
• Rodinná pouta
• Rodinný film
• Rodino Oneiro
• Rodino, Rodinsky District, Altai Krai
• Rodin Quiñones
• Rodin Quiñónes
• Rodinsky Municipal District
• Rodin Thoma
• Rodion Alimov
• Rodion Cantacuzino
• Rodion Kazakov
• Rodion Nakhapetov
• Rodionovka
• Rodionov, Kirill
• Rodionov message