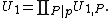“Leopoldt's conjecture”的意思、由来-开放百科全书

词条

Leopoldt's conjecture

释义

Formulation
References

In algebraic number theory, Leopoldt's conjecture, introduced by {{harvs|txt|authorlink=Heinrich-Wolfgang Leopoldt|first=H.-W. |last=Leopoldt|year1=1962|year2=1975}}, states that the p-adic regulator of a number field does not vanish. The p-adic regulator is an analogue of the usual

regulator defined using p-adic logarithms instead of the usual logarithms, introduced by {{harvs|txt|authorlink=Heinrich-Wolfgang Leopoldt|first=H.-W. |last=Leopoldt|year=1962}}.

Leopoldt proposed a definition of a p-adic regulator R_p attached to K and a prime number p. The definition of R_p uses an appropriate determinant with entries the p-adic logarithm of a generating set of units of K (up to torsion), in the manner of the usual regulator. The conjecture, which for general K is still open {{as of|2009|lc=}}, then comes out as the statement that R_p is not zero.

Formulation

Let K be a number field and for each prime P of K above some fixed rational prime p, let U_P denote the local units at P and let U_1,P denote the subgroup of principal units in U_P. Set

Then let E₁ denote the set of global units ε that map to U₁ via the diagonal embedding of the global units in E.

Since is a finite-index subgroup of the global units, it is an abelian group of rank 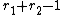, where is the number of real embeddings of and the number of pairs of complex embeddings. Leopoldt's conjecture states that the 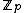-module rank of the closure of embedded diagonally in 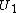is also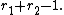

Leopoldt's conjecture is known in the special case where is an abelian extension of or an abelian extension of an imaginary quadratic number field: {{harvtxt|Ax|1965}} reduced the abelian case to a p-adic version of Baker's theorem, which was proved shortly afterwards by {{harvtxt|Brumer|1967}}.

{{harvs|txt|authorlink=Preda Mihăilescu|last=Mihăilescu|year1=2009|year2=2011}} has announced a proof of Leopoldt's conjecture for all CM-extensions of

.{{harvs|txt|authorlink=Pierre Colmez|last=Colmez|year=1988}} expressed the residue of the p-adic Dedekind zeta function of a totally real field at s = 1 in terms of the p-adic regulator. As a consequence, Leopoldt's conjecture for those fields is equivalent to their p-adic Dedekind zeta functions having a simple pole at s = 1.

References

{{Citation | last1=Ax | first1=James | title=On the units of an algebraic number field | url=http://projecteuclid.org/euclid.ijm/1256059299 | mr=0181630 | year=1965 | journal=Illinois Journal of Mathematics | issn=0019-2082 | volume=9 | pages=584–589 | zbl=0132.28303 }}
{{Citation | last1=Brumer | first1=Armand | title=On the units of algebraic number fields | doi=10.1112/S0025579300003703 | mr=0220694 | year=1967 | journal=Mathematika. A Journal of Pure and Applied Mathematics | issn=0025-5793 | volume=14 | issue=2 | pages=121–124 | zbl=0171.01105 }}
{{Citation | last1=Colmez | first1=Pierre | title=Résidu en s=1 des fonctions zêta p-adiques | doi=10.1007/BF01389373 | mr=922806 | year=1988 | journal=Inventiones Mathematicae | issn=0020-9910 | volume=91 | issue=2 | pages=371–389 | zbl=0651.12010 | bibcode=1988InMat..91..371C }}
{{eom|id=l/l110120|first=M.|last= Kolster}}
{{Citation | last1=Leopoldt | first1=Heinrich-Wolfgang | authorlink=Heinrich-Wolfgang Leopoldt | title=Zur Arithmetik in abelschen Zahlkörpern | url=http://resolver.sub.uni-goettingen.de/purl?GDZPPN002179482 | mr=0139602 | year=1962 | journal=Journal für die reine und angewandte Mathematik | issn=0075-4102 | volume=209 | pages=54–71 | zbl=0204.07101 }}
{{Citation |first=H. W. |last=Leopoldt | authorlink=Heinrich-Wolfgang Leopoldt |title=Eine p-adische Theorie der Zetawerte II |journal=Journal für die reine und angewandte Mathematik |volume=1975 |year=1975 |issue=274/275 |pages=224–239 |doi=10.1515/crll.1975.274-275.224 | zbl=0309.12009 }}.
{{Citation |last=Mihăilescu |first=Preda |year=2009 |title=The T and T components of Λ - modules and Leopoldt's conjecture |journal=|volume= |issue= |pages= |arxiv=0905.1274 |bibcode=2009arXiv0905.1274M}}
{{Citation|last=Mihăilescu |first=Preda |year=2011|arxiv=1105.4544 |title=Leopoldt's Conjecture for CM fields|bibcode=2011arXiv1105.4544M}}
{{Neukirch et al. CNF|edition=2}}
{{Citation |first=Lawrence C. |last=Washington |title=Introduction to Cyclotomic Fields |edition=Second |year=1997 |location=New York |publisher=Springer |isbn=0-387-94762-0 | zbl=0966.11047 }}.

2 : Algebraic number theory|Conjectures

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。