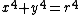- References
where 
.[1] It looks like a rounded square with "sides" of length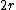 
and centered on the origin. This curve is a squircle centered on the origin, and it is a special case of a superellipse.[2]
Because of Pierre de Fermat's only surviving proof, that of the n = 4 case of Fermat's Last Theorem, if r is rational there is no non-trivial rational point (x, y) on this curve (that is, no point for which both x and y are non-zero rational numbers).
References
1. ^{{citation|title=Analytic Geometry Problems|volume=108|series=College Outline Series|first=Cletus Odia|last=Oakley|publisher=Barnes & Noble|year=1958|page=171}}.
2. ^{{citation|title=The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English|series=MAA Spectrum|first=Steven|last=Schwartzman|publisher=Mathematical Association of America|year=1994|isbn=9780883855119|page=212|url=https://books.google.com/books?id=SRw4PevE4zUC&pg=PA212}}.
{{DEFAULTSORT:Lame's special quartic}}{{algebraic-geometry-stub}}2. ^{{citation|title=The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English|series=MAA Spectrum|first=Steven|last=Schwartzman|publisher=Mathematical Association of America|year=1994|isbn=9780883855119|page=212|url=https://books.google.com/books?id=SRw4PevE4zUC&pg=PA212}}.
1 : Equations
- Newt gunray
- Newt Gunray
- New Thacker, West Virginia
- Newt Halliday
- New Thang
- New Theatre Comique
- New Theatre (Exeter)
- New Theatre (Fort Smith, Arkansas)
- New Theatre (Nottingham)
- New Theatre (Plzeň)
- New theatre royal
- New Theatre Royal
- New Theatre Royal, Portsmouth
- New Theatres Calcutta
- New Thebes
- New Thessaloniki Railway Station
- New Thing (Redfoo song)
- New Thing (Rye Rye song)
- New Thought movement
- New Three Major Night Views of Japan
- New Three Night Views of Japan
- Newt Hudson
- New timeline
- New Times Inc.
- New Times L.A.