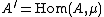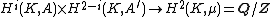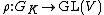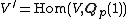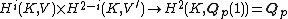“Local Tate duality”的意思、由来-开放百科全书

词条

Local Tate duality

释义

Statement
Case of finite modules Case of p-adic representations
See also
Notes
References

In Galois cohomology, local Tate duality (or simply local duality) is a duality for Galois modules for the absolute Galois group of a non-archimedean local field. It is named after John Tate who first proved it. It shows that the dual of such a Galois module is the Tate twist of usual linear dual. This new dual is called the (local) Tate dual.

Local duality combined with Tate's local Euler characteristic formula provide a versatile set of tools for computing the Galois cohomology of local fields.

Statement

Let K be a non-archimedean local field, let K^s denote a separable closure of K, and let G_K = Gal(K^s/K) be the absolute Galois group of K.

Case of finite modules

Denote by μ the Galois module of all roots of unity in K^s. Given a finite G_K-module A of order prime to the characteristic of K, the Tate dual of A is defined as

(i.e. it is the Tate twist of the usual dual A^∗). Let Hⁱ(K, A) denote the group cohomology of G_K with coefficients in A. The theorem states that the pairing

given by the cup product sets up a duality between Hⁱ(K, A) and H²⁻ⁱ(K, A^′) for i = 0, 1, 2.^[1] Since G_K has cohomological dimension equal to two, the higher cohomology groups vanish.^[2]

Case of p-adic representations

Let p be a prime number. Let Q_p(1) denote the p-adic cyclotomic character of G_K (i.e. the Tate module of μ). A p-adic representation of G_K is a continuous representation

where V is a finite-dimensional vector space over the p-adic numbers Q_p and GL(V) denotes the group of invertible linear maps from V to itself.^[3] The Tate dual of V is defined as

(i.e. it is the Tate twist of the usual dual V^∗ = Hom(V, Q_p)). In this case, Hⁱ(K, V) denotes the continuous group cohomology of G_K with coefficients in V. Local Tate duality applied to V says that the cup product induces a pairing

which is a duality between Hⁱ(K, V) and H²⁻ⁱ(K, V ′) for i = 0, 1, 2.^[4] Again, the higher cohomology groups vanish.

Notes

1. ^{{harvnb|Serre|2002|loc=Theorem II.5.2}}
2. ^{{harvnb|Serre|2002|loc=§II.4.3}}
3. ^Some authors use the term p-adic representation to refer to more general Galois modules.
4. ^{{harvnb|Rubin|2000|loc=Theorem 1.4.1}}

References

{{Citation

| last=Rubin
| first=Karl
| author-link=Karl Rubin
| title=Euler systems
| publisher=Princeton University Press
| year=2000
| series=Hermann Weyl Lectures, Annals of Mathematics Studies
| volume=147
| mr=1749177
| isbn=978-0-691-05076-8
}}

{{Citation | last1=Serre | first1=Jean-Pierre | author1-link= Jean-Pierre Serre | title=Galois cohomology | publisher=Springer-Verlag | location=Berlin, New York | series=Springer Monographs in Mathematics | isbn=978-3-540-42192-4 | mr=1867431 | year=2002}}, translation of Cohomologie Galoisienne, Springer-Verlag Lecture Notes 5 (1964).

3 : Theorems in algebraic number theory|Galois theory|Duality theories

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Statement

Case of finite modules

Case of p-adic representations

See also

Notes

References