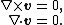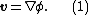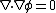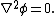“Laplacian vector field”的意思、由来-开放百科全书

词条

Laplacian vector field

释义

See also

In vector calculus, a Laplacian vector field is a vector field which is both irrotational and incompressible. If the field is denoted as v, then it is described by the following differential equations:

From the vector calculus identity 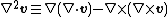it follows that

that is, that the field v satisfies Laplace's equation.

A Laplacian vector field in the plane satisfies the Cauchy–Riemann equations: it is holomorphic.

Since the curl of v is zero, it follows that (when the domain of definition is simply connected) v can be expressed as the gradient of a scalar potential (see irrotational field) φ :

Then, since the divergence of v is also zero, it follows from equation (1) that

which is equivalent to

Therefore, the potential of a Laplacian field satisfies Laplace's equation.

See also