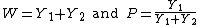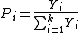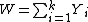“Lukacs's proportion-sum independence theorem”的意思、由来-开放百科全书

词条

Lukacs's proportion-sum independence theorem

释义

The theorem
Corollary
References

In statistics, Lukacs's proportion-sum independence theorem is a result that is used when studying proportions, in particular the Dirichlet distribution. It is named for Eugene Lukacs.^[1]

The theorem

If Y₁ and Y₂ are non-degenerate, independent random variables, then the random variables

are independently distributed if and only if both Y₁ and Y₂ have gamma distributions with the same scale parameter.

Corollary

Suppose Y_i, i = 1, ..., k be non-degenerate, independent, positive random variables. Then each of k − 1 random variables

is independent of

if and only if all the Y_i have gamma distributions with the same scale parameter.^[2]

References

1. ^{{Cite journal|doi= 10.1214/aoms/1177728549|author= Lukacs, Eugene|title=A characterization of the gamma distribution|journal=Annals of Mathematical Statistics|volume=26|year=1955|pages=319–324}}
2. ^{{cite journal| last=Mosimann| first=James E.| title=On the compound multinomial distribution, the multivariate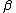

distribution, and correlation among proportions| journal=Biometrika| year=1962| volume=49| issue=1 and 2|pages=65–82|jstor=2333468| doi=10.1093/biomet/49.1-2.65}}

{{cite book|last1=Ng| first1=W. N.|last2=Tian| first2=G-L| last3=Tang| first3=M-L| title=Dirichlet and Related Distributions| publisher=John Wiley & Sons, Ltd.| year=2011|isbn=978-0-470-68819-9}} page 64. [https://books.google.com/books?id=k8GS868oyo4C&pg=PT81&dq#v=onepage&q&f=false Lukacs's proportion-sum independence theorem and the corollary] with a proof.

2 : Probability theorems|Characterization of probability distributions

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。