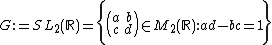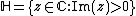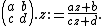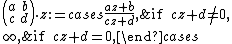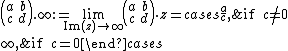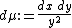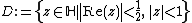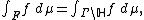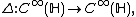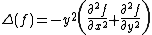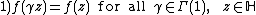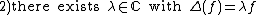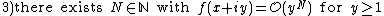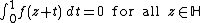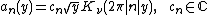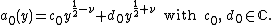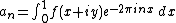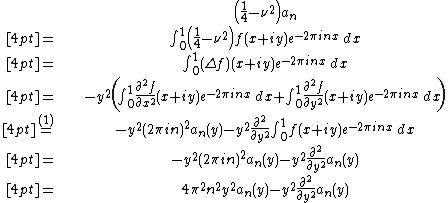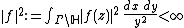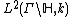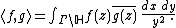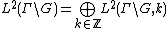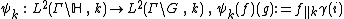- General remarks
- Classic Maass wave forms Definition of the hyperbolic Laplace operator Definition of a Maass wave form Relation between Maass wave forms and Dirichlet series Theorem : The Fourier coefficients of a Maass wave form Theorem: The L-Function of a Maass wave form
- Example: The non-holomorphic Eisenstein-series E Theorem: E is a Maass waveform Proposition: E is
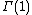 - invariant Proposition : E is an eigenform of the hyperbolic Laplace operator Theorem : The Fourier-expansion of E
- invariant Proposition : E is an eigenform of the hyperbolic Laplace operator Theorem : The Fourier-expansion of E - Maas wave forms of weight k Congruence subgroups Definition: Maass wave forms of weight The spectral problem Embedding into the space
- Maass cusp form Definition Major results Higher dimensions
- Automorphic representations of the adele group The Group
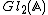 Adelisation of Cuspforms Cusp forms of the adele group Cuspial representations of the adele group Automorphic L-Functions
Adelisation of Cuspforms Cusp forms of the adele group Cuspial representations of the adele group Automorphic L-Functions - See also
- References
In mathematics, Maass wave forms or Maass forms are studied in the theory of automorphic forms. Maass wave forms are complex-valued smooth functions of the upper half plane, which transform in a similar way under the operation of a discrete subgroup  of
of 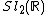 as modular forms. They are Eigenforms of the hyperbolic Laplace Operator
as modular forms. They are Eigenforms of the hyperbolic Laplace Operator  defined on
defined on 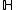 and satisfy certain growth conditions at the cusps of a fundamental domain of
and satisfy certain growth conditions at the cusps of a fundamental domain of  . In contrast to the modular forms the Maass wave forms need not be holomorphic. They were studied first by Hans Maass in 1949.
. In contrast to the modular forms the Maass wave forms need not be holomorphic. They were studied first by Hans Maass in 1949.
General remarks
The group
operates on the upper half plane
by fractional linear transformations :
It can be extended to an operation on 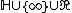 by defining :
by defining :
The Radon measure
defined on 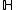 is invariant under the operation of
is invariant under the operation of 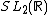 .
.
Let  be a discrete subgroup of
be a discrete subgroup of  . A fundamental domain for
. A fundamental domain for  is an open set
is an open set 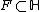 , so that there exists a system of representatives
, so that there exists a system of representatives  of
of 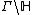 with
with
A fundamental domain for the modular group 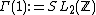 is given by
is given by
(see Modular form).
A function 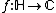 is called
is called  -invariant, if
-invariant, if 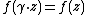 holds for all
holds for all  and all
and all 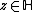 .
.
For every measurable,  -invariant function
-invariant function 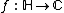 the equation
the equation
holds. Here the measure 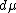 on the right side of the equation is the induced measure on the quotient
on the right side of the equation is the induced measure on the quotient 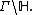
Classic Maass wave forms
Definition of the hyperbolic Laplace operator
The hyperbolic Laplace operator on 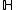 is defined as
is defined as
Definition of a Maass wave form
A Maass wave form for the group 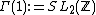 is a complex-valued smooth function
is a complex-valued smooth function  on
on 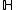 so that
so that
If
we call  Maass cusp form.
Maass cusp form.
Relation between Maass wave forms and Dirichlet series
Let  be a Maass wave form. Since
be a Maass wave form. Since 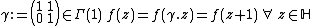 ,
,
 has a Fourier-expansion of the form
has a Fourier-expansion of the form
 ,
,
with coefficient functions 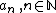 .
.
It is easy to show that  is Maass cusp form if and only if
is Maass cusp form if and only if 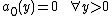 .
.
We can calculate the coefficient functions in a precise way. For this we need the Bessel function  .
.
Definition: The Bessel function  is defined as
is defined as
 .
.
The integral converges locally uniformly absolutely for  in
in 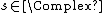 and the inequality
and the inequality
 holds for all
holds for all 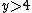 .
.
Therefore, 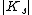 decreases exponentially for
decreases exponentially for 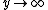 . Furthermore, we have
. Furthermore, we have 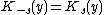 for all
for all 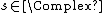 ,
,  .
.
Theorem : The Fourier coefficients of a Maass wave form
Let 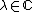 be the eigenvalue of the Maass wave form f corresponding to
be the eigenvalue of the Maass wave form f corresponding to . There is a
. There is a 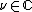 which is unique up to sign such that
which is unique up to sign such that 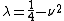 . Then the Fourier coefficients of
. Then the Fourier coefficients of  are
are
if 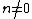 . If
. If 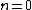 we get
we get
Proof: We have 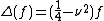 . By the definition of the Fourier coefficients we get
. By the definition of the Fourier coefficients we get
for 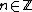 .
.
Together it follows that
for 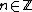 .
.
In (1) we used that the nth Fourier coefficient of 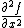 is
is 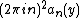 for the first summation term. In the second term we changed the order of integration and differentiation, which is allowed since f is smooth in y . We get a linear differential equation of second degree :
for the first summation term. In the second term we changed the order of integration and differentiation, which is allowed since f is smooth in y . We get a linear differential equation of second degree :

For 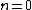 one can show, that for every solution
one can show, that for every solution  there exist unique coefficients
there exist unique coefficients
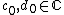 with the property
with the property 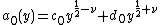 .
.
For 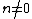 every solution
every solution  is of the form
is of the form

for unique 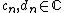 . Here
. Here 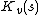 and
and 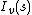 are Bessel functions.
are Bessel functions.
The Bessel functions 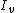 grow exponentially, while the Bessel functions
grow exponentially, while the Bessel functions  decrease exponentially. Together with the polynomial growth condition 3) we get
decrease exponentially. Together with the polynomial growth condition 3) we get 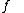 :
: 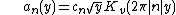 (also
(also 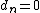 ) for a unique
) for a unique 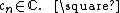
Even and odd Maass Waveforms : Let 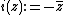 . Then i operates on all functions
. Then i operates on all functions 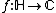 by
by 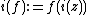 . i commutes with the hyperbolic Laplacian. A Maass wave form
. i commutes with the hyperbolic Laplacian. A Maass wave form  is called even, if
is called even, if 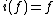 and odd if
and odd if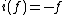 . If f is a Maass wave form, then
. If f is a Maass wave form, then 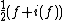 is an even Maass wave form and
is an even Maass wave form and 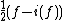 an odd Maass wave form and it holds that
an odd Maass wave form and it holds that 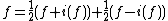 .
.
Theorem: The L-Function of a Maass wave form
Let 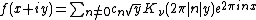 be a Maass cusp form. We define the L-function L of
be a Maass cusp form. We define the L-function L of  as
as
 .
.
Then the series 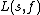 converges for
converges for 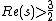 and we can continue it to a whole function on
and we can continue it to a whole function on 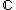 .
.
If f is even or odd we get
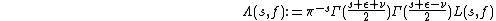 .
.
Here 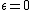 if
if  is even and
is even and 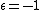 if
if  is odd. Then
is odd. Then  satisfies the functional equation
satisfies the functional equation
 .
.
Example: The non-holomorphic Eisenstein-series E
The non-holomorphic Eisenstein-series is defined for 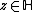 and
and 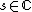 as
as
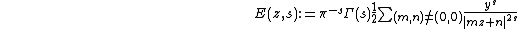
where 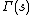 is the Gamma function.
is the Gamma function.
The series converges absolutely in 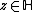 for
for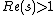 and locally uniformly in
and locally uniformly in 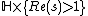 , since one can show, that the series
, since one can show, that the series
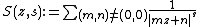 converges absolutely in
converges absolutely in 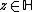 , if
, if 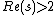 . More precisely it converges uniformly on every set
. More precisely it converges uniformly on every set 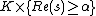 , for every compact set
, for every compact set 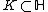 and every
and every  .
.
Theorem: E is a Maass waveform
We only show 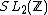 - invariance and the differential equation. A proof of the smoothness can be found in Deitmar or Bump. The growth condition follows from the theorem of the Fourier-expansion of E.
- invariance and the differential equation. A proof of the smoothness can be found in Deitmar or Bump. The growth condition follows from the theorem of the Fourier-expansion of E.
We will first show the 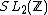 - invariance. Let
- invariance. Let

be the stabilizer group  corresponding to the operation of
corresponding to the operation of 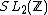 on
on 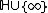 . Then the following Lemma holds :
. Then the following Lemma holds :
Lemma: The map
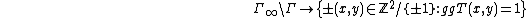

is a bijection.
Proposition: E is 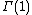 - invariant
- invariant
(a) Let 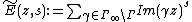 . Then
. Then 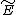 converges absolutely in
converges absolutely in 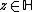 for
for 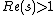 and it holds that
and it holds that
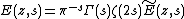 .
.
(b) We have 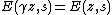 for all
for all 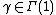 .
.
(a): For 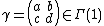 it holds that
it holds that 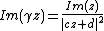 . Therefore, we obtain
. Therefore, we obtain
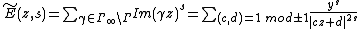
by using the Lemma.
That proves the absolute convergence in 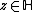 for
for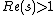 .
.
Furthermore, it follows that
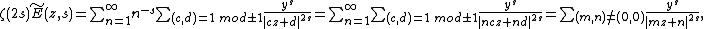
since the map 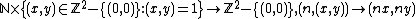 is a bijection.
is a bijection.
(a) follows.
(b): For 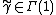 we get
we get
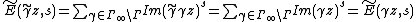 .
.
Together with (a),  is also invariant under
is also invariant under 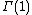 .
. 
Proposition : E is an eigenform of the hyperbolic Laplace operator
We need the following Lemma :
Lemma: commutes with the operation of
commutes with the operation of  on
on 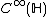 . More precisely
. More precisely 
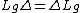
holds for all 
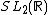 is generated by the elements of the form
is generated by the elements of the form 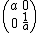 with
with 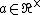 and
and 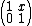 with
with 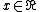 and
and 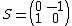 . One calculates the claim for these generators and obtains the claim for all
. One calculates the claim for these generators and obtains the claim for all 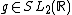 .
. 
Since  it is sufficient to show the differential equation for
it is sufficient to show the differential equation for 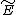 .
.
It holds that
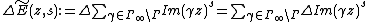
Furthermore, one has
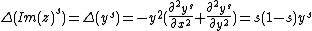 .
.
Since the Laplace Operator commutes with the Operation of 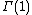 , we get
, we get
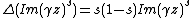 and so
and so 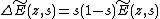 .
.
for all 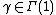 .
.
Therefore, the differential equation holds for E in 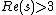 . In order to obtain the claim for all
. In order to obtain the claim for all 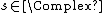 , consider the function
, consider the function
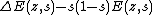 . By explicitly calculating the Fourier expansion of this function, we get that it is meromorphic. Since it vanishes for
. By explicitly calculating the Fourier expansion of this function, we get that it is meromorphic. Since it vanishes for 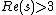 , it must be the zero function by the Identity theorem.
, it must be the zero function by the Identity theorem.
Theorem : The Fourier-expansion of E
The nonholomorphic Eisenstein series has a Fourier expansion

where
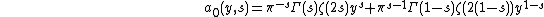
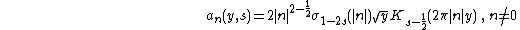 .
.
If 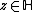 ,
, 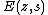 has a meromorphic continuation on
has a meromorphic continuation on  . It is holomorphic except for simple poles at
. It is holomorphic except for simple poles at 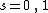 .
.
The Eisenstein series satisfies the functional equation

for all 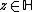 .
.
Locally uniformly in 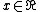 the growth condition
the growth condition

holds, where 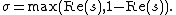
The meromorphic continuation of E is very important in the spectral theory of the hyperbolic Laplace Operator.
Maas wave forms of weight k
Congruence subgroups
For 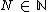 let
let 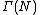 be the kernel of the canonical projection
be the kernel of the canonical projection
 .
.
We call 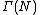 principal congruence subgroup of level
principal congruence subgroup of level  .
.
A subgroup 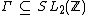 is called congruence subgroup, if there exists
is called congruence subgroup, if there exists 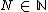 , so that
, so that 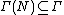 .
.
All congruence subgroups are discrete.
Let 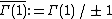 . For a congruence subgroup
. For a congruence subgroup  ,let
,let 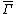 be the image of
be the image of  in
in  .
.
If S is a system of representatives of 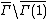 , then
, then

is a fundamental domain for  . The set
. The set  is uniquely determined by the fundamental domain
is uniquely determined by the fundamental domain 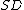 . Furthermore,
. Furthermore,  is finite.
is finite.
The points 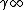 for
for 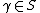 are called cusps of the fundamental domain
are called cusps of the fundamental domain 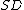 . They are a subset of
. They are a subset of 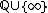 .
.
For every cusp  there exists
there exists 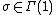 with
with 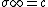 .
.
Definition: Maass wave forms of weight
Let  be a congruence subgroup and
be a congruence subgroup and 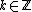 .
.
We define the hyperbolic Laplace operator 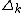 of weight
of weight  as
as
 ,
,

This is a generalization of the hyperbolic Laplace operator 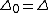 .
.
We define an operation of 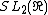 on
on  by
by

where 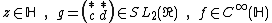 .
.
It can be shown, that

holds for all 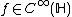 ,
, 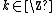 and every
and every 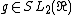 .
.
Therefore, 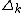 operates on the vector space
operates on the vector space
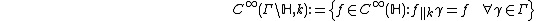 .
.
Definition : A Maass wave form of weight 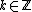 for the group
for the group  is a function
is a function 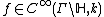 , which is an Eigenform of
, which is an Eigenform of 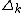 and is of moderate growth at the cusps.
and is of moderate growth at the cusps.
The term moderate growth at cusps will need clarification :
Let  be a congruence subgroup. Then
be a congruence subgroup. Then  is a cusp and we say that a function
is a cusp and we say that a function  aus
aus 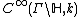 is of moderate growth at
is of moderate growth at  , if
, if  is bounded by a polynomial in y for
is bounded by a polynomial in y for 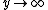 . Let
. Let 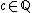 be another cusp . Then there exists ein
be another cusp . Then there exists ein 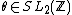 with
with 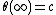 . Let
. Let 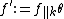 . One calculates, that
. One calculates, that  is an element of
is an element of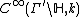 , where
, where 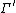 is the congruence subgroup
is the congruence subgroup 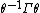 . We say
. We say  is of moderate growth at the cusp
is of moderate growth at the cusp  , if
, if  is of moderate growth at
is of moderate growth at  .
.
If contains a principal congruence subgroup of level
contains a principal congruence subgroup of level  , we say that
, we say that  is cuspidal at infinity, if
is cuspidal at infinity, if
 holds for all
holds for all 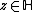 .
.
We say that  is cuspidal at the cusp
is cuspidal at the cusp  , if
, if  is cuspidal at infinity.
is cuspidal at infinity.
If  is cuspidal at every cusp, we call
is cuspidal at every cusp, we call  cusp form.
cusp form.
Cuspidal Maass wave forms are called Maass cusp forms.
We give a simple example of a Maass wave form of weight 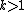 for the modular group :
for the modular group :
Example : Let  be a modular form of weight
be a modular form of weight 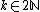 for the group
for the group 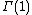 . Then
. Then 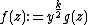 is a Maass wave form of weight
is a Maass wave form of weight  for the group
for the group 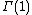 .
.
The spectral problem
Let  be a congruence subgroup of
be a congruence subgroup of 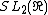 .
.
and let 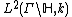 be the vector space of all measurable functions
be the vector space of all measurable functions 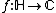 with
with 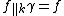 for all
for all  .
.
Furthermore, define the vector space
modulo functions with 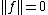 . The integral is well definded, since the function
. The integral is well definded, since the function 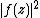 is
is  - invariant.
- invariant.
a Hilbert space with scalar product
The operator 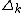 can be defined in a vector space
can be defined in a vector space 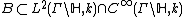 which is dense in
which is dense in 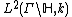 . There
. There 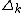 is a positive semidefinite symmetric operator. It can be shown, that there exists a unique selfadjoint continuation on
is a positive semidefinite symmetric operator. It can be shown, that there exists a unique selfadjoint continuation on 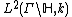 .
.
We define 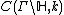 as the space of all cusp forms
as the space of all cusp forms 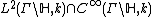 .
.
Then 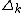 operates on
operates on 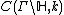 and has a discrete spectrum. The spectrum belonging to the orthogonal complement has a continuous part and can be described with the help of (modified) non-holomorphic Eisenstein series, their meromorphic continuations and their residues. (See Bump or Iwaniec) .
and has a discrete spectrum. The spectrum belonging to the orthogonal complement has a continuous part and can be described with the help of (modified) non-holomorphic Eisenstein series, their meromorphic continuations and their residues. (See Bump or Iwaniec) .
If  is a discrete (torsionfree) subgroup of
is a discrete (torsionfree) subgroup of 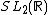 , so that the quotient
, so that the quotient 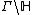 is compact, the spectral problem simplifies. This is because a discrete cocompact subgroup has no cusps. Here all of the space
is compact, the spectral problem simplifies. This is because a discrete cocompact subgroup has no cusps. Here all of the space 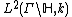 is a sum of eigenspaces.
is a sum of eigenspaces.
Embedding into the space 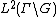
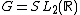 is a unimodular locally compact group with the topology of
is a unimodular locally compact group with the topology of  .
.
Let  be a congruence subgroup. Since
be a congruence subgroup. Since  is discrete in
is discrete in  ,
,  is closed in
is closed in  . The group
. The group  is unimodular and since the counting measure is a Haar-measure on the discrete group
is unimodular and since the counting measure is a Haar-measure on the discrete group  ,
,  is also unimodular. By the Quotient Integral Formula there exists a
is also unimodular. By the Quotient Integral Formula there exists a  - right-invariant Radon measure
- right-invariant Radon measure  on the locally compact space
on the locally compact space  . Let
. Let 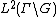 be the corresponding
be the corresponding  - space.
- space.
The space 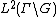 decomposes into a Hilbert space direct sum
decomposes into a Hilbert space direct sum
where 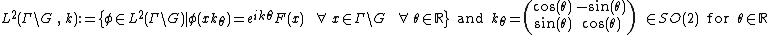 .
.
The Hilbert-space 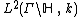 can be embedded isometrically into the Hilbert space
can be embedded isometrically into the Hilbert space 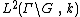 . The isometry is given by the map
. The isometry is given by the map
Therefore, all Maass cusp forms for the congruence group  can be thought of as elements of
can be thought of as elements of 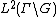 .
.
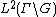 is a Hilbert space carrying an operation of the group
is a Hilbert space carrying an operation of the group  , the so-called right regular representation :
, the so-called right regular representation :
One can easily show, that  is a unitary representation of
is a unitary representation of  on the Hilbert space
on the Hilbert space 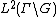 . One is interested in a decomposition into irreducible suprepresentations. This is only possible if
. One is interested in a decomposition into irreducible suprepresentations. This is only possible if  is cocompact. If not, there is also a continuous Hilbert-integral part. The interesting part is, that the solution of this problem also solves the spectral problem of Maass wave forms. (see Bump, C. 2.3)
is cocompact. If not, there is also a continuous Hilbert-integral part. The interesting part is, that the solution of this problem also solves the spectral problem of Maass wave forms. (see Bump, C. 2.3)
Maass cusp form
A Maass cusp form, a subset of Maass wave forms, is a function on the upper half-plane that transforms like a modular form but need not be holomorphic. They were first studied by Hans Maass in {{harvtxt|Maass|1949}}.
Definition
Let k be an integer, s be a complex number, and Γ be a discrete subgroup of SL2(R). A Maass form of weight k for Γ with Laplace eigenvalue s is a smooth function from the upper half-plane to the
complex numbers satisfying the following conditions:
- For all
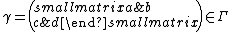 and all
and all 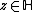 , we have
, we have 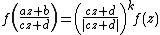 .
. - We have
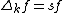 , where
, where 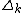 is the weight k hyperbolic Laplacian defined as
is the weight k hyperbolic Laplacian defined as
- The function ƒ is of at most polynomial growth at cusps.
A weak Maass form is defined similarly but with the third condition replaced by "The function ƒ has at most linear exponential growth at cusps". Moreover, ƒ is said to be harmonic if it is annihilated by the Laplacian operator.
Major results
Let ƒ be a weight 0 Maass cusp form. Its normalized Fourier coefficient at a prime p is bounded by p7/64 + p−7/64. This theorem is due to Henry Kim and Peter Sarnak. It is an approximation toward Ramanujan-Petersson conjecture.
Higher dimensions
Maass cusp forms can be regarded as automorphic forms on GL(2). It is natural to define Maass cusp forms on GL(n) as spherical automorphic forms on GL(n) over the rational number field. Their existence is proved by Miller, Mueller, etc.
Automorphic representations of the adele group
The Group 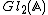
Let  be a commutative ring with unit and let
be a commutative ring with unit and let 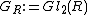 be the group of
be the group of  matrices with entries in
matrices with entries in  and invertible determinant .
and invertible determinant .
Let 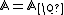 be the ring of rational adeles,
be the ring of rational adeles, 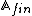 the ring of the finite (rational) adeles and for a prime number
the ring of the finite (rational) adeles and for a prime number 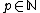 let
let 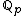 be the field of p-adic numbers. Furthermore, let
be the field of p-adic numbers. Furthermore, let 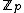 be the ring of the p-adic integers (see Adele ring).
be the ring of the p-adic integers (see Adele ring).
Define 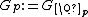 . Both
. Both 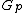 and
and 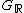 are locally compact unimodular groups if one equips them with the subspace topologies of
are locally compact unimodular groups if one equips them with the subspace topologies of 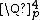 respectively
respectively  .
.
The group 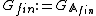 is isomorphic to the group
is isomorphic to the group 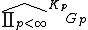 . Here the product is the resctricted product
. Here the product is the resctricted product 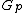 , concerning the compact, open subgroups
, concerning the compact, open subgroups 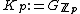 of
of 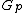 . Then
. Then 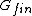 locally compact group, if we equip it with the restricted product topology.
locally compact group, if we equip it with the restricted product topology.
The group 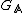 is isomorphic to the group
is isomorphic to the group

and is a locally compact group with the product topology, since 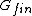 and
and 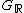 are both locally compact.
are both locally compact.
Let 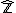 be the ring
be the ring 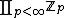 . The subgroup
. The subgroup

is a maximal compact, open subgroup of 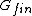 and can be thought of as a subgroup of
and can be thought of as a subgroup of 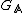 , when we consider the embedding
, when we consider the embedding 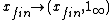 .
.
We define 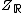 as the center of
as the center of  , that means
, that means 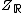 is the group of all diagonal matrices of the form
is the group of all diagonal matrices of the form 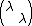 , where
, where 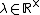 . We think of
. We think of 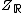 as a subgroup of
as a subgroup of 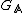 since we can embed the group by
since we can embed the group by 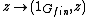 .
.
The group 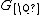 is embedded diagonally in
is embedded diagonally in 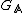 , which is possible, since all four entries of a
, which is possible, since all four entries of a 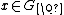 can only have finite amount of prime divisors and therefore
can only have finite amount of prime divisors and therefore  for all but finitely many prime numbers
for all but finitely many prime numbers 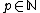 .
.
Let 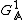 be the group of all
be the group of all 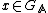 with
with 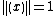 . (see Adele Ring for a definition of the absolute value of an Idele). One can easily calculate, that
. (see Adele Ring for a definition of the absolute value of an Idele). One can easily calculate, that 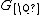 is a subgroup of
is a subgroup of 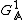 .
.
With the one-to-one map 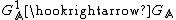 we can identify the groups
we can identify the groups 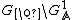 and
and 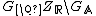 with each other.
with each other.
The group 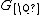 is dense in
is dense in 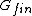 and discrete in
and discrete in 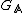 . The Quotient
. The Quotient 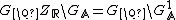 is not compact but has finite Haar-measure.
is not compact but has finite Haar-measure.
Therefore, 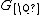 is a lattice of
is a lattice of 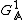 , similar to the classical case of the modular group and
, similar to the classical case of the modular group and 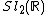 . By harmonic analysis one also gets that
. By harmonic analysis one also gets that 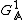 is unimodular.
is unimodular.
Adelisation of Cuspforms
We now want to embed the classical Maass cusp forms of weight 0 for the modular group into 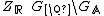 . This can be achieved with the "strong approximationtheorem", which states, that the map
. This can be achieved with the "strong approximationtheorem", which states, that the map

is a 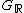 - equivariant homeomorphism. So we get
- equivariant homeomorphism. So we get

and furthermore
 .
.
Maass cuspforms of weight 0 for modular group can be embedded into
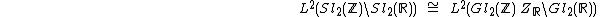 .
.
By the strong approximation theorem this space is unitary isomorphic to
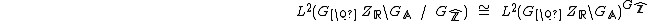
which is a subspace of 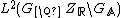 .
.
In the same way one can embed the classical holomorphic cusp forms. With a small generalization of the approximation theorem, one can embed all Maass cusp forms (as well as the holomorphic cuspforms) of any weight for any congruence subgroup  in
in 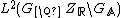 .
.
We call 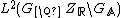 the space of automorphic forms of the adele group.
the space of automorphic forms of the adele group.
Cusp forms of the adele group
Let  be a Ring and let
be a Ring and let  be the group of all
be the group of all 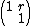 ,
,
where 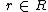 . This group is isomorphic to the additive group of R.
. This group is isomorphic to the additive group of R.
We call a function 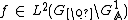 cusp form, if
cusp form, if

holds for almost all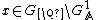 . Let
. Let 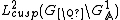 (or just
(or just 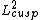 ) be the vectorspace of these cusp forms.
) be the vectorspace of these cusp forms. 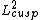 is a closed subspace of
is a closed subspace of 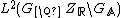 and it is invariant under the right regular representation of
and it is invariant under the right regular representation of 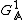 .
.
One is again intereseted in a decomposition of 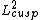 into irreducible closed subspaces .
into irreducible closed subspaces .
We have the following theorem :
The space 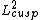 decomposes in a direct sum of irreducible Hilbert-spaces with finite multiplicities
decomposes in a direct sum of irreducible Hilbert-spaces with finite multiplicities 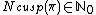 :
:

The calculation of these multiplicities 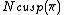 is one of the most important and most difficult problems in the theory of automorphic forms.
is one of the most important and most difficult problems in the theory of automorphic forms.
Cuspial representations of the adele group
An irreducible representation  of the group
of the group 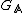 is called cuspidal, if it is isomorphic to a subrepresentation of
is called cuspidal, if it is isomorphic to a subrepresentation of 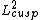 ist.
ist.
An irreducible representation  of the group
of the group 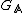 is called admissible if there exists a compact subgroup
is called admissible if there exists a compact subgroup  of
of 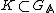 , so that
, so that 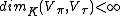 for all
for all 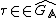 .
.
One can show, that every cuspidal representation is admissible.
The admissibility is needed to proof the so-called Tensorprodukt-Theorem anzuwenden, which says, that every irreducible, unitary and admissible representation of the group 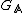 is isomorphic to an infinite tensor product
is isomorphic to an infinite tensor product
 .
.
The 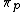 are irreducible representations of the group
are irreducible representations of the group 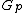 . Almost all of them need to be umramified.
. Almost all of them need to be umramified.
(A representation 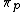 of the group
of the group 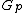
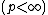 is called unramified, if the vector space
is called unramified, if the vector space

is not the zero space.)
A construction of an infinite tensor product can be found in Deitmar,C.7.
Automorphic L-Functions
Let  be an irreducible, admissible unitary representation of
be an irreducible, admissible unitary representation of 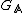 . By the tensor product theorem,
. By the tensor product theorem,  is of the form
is of the form 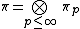 (see cuspidal representations of the adele group)
(see cuspidal representations of the adele group)
Let  be a finite set of places containing
be a finite set of places containing  and all ramified places . One defines the global Hecke - function of
and all ramified places . One defines the global Hecke - function of  as
as

where 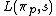 is a so-called local L - function of the local representation
is a so-called local L - function of the local representation 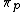 . A construction of local L - functions can be found in Deitmar C. 8.2.
. A construction of local L - functions can be found in Deitmar C. 8.2.
If  is a cuspidal representation, the L-Funktion
is a cuspidal representation, the L-Funktion 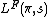 has a meromorphic continuation on
has a meromorphic continuation on 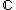 . This is possible, since
. This is possible, since 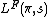 , satisfies certain functional equations.
, satisfies certain functional equations.
See also
- Harmonic Maass form
- Mock modular form
- Real analytic Eisenstein series
- Automorphic form
- Modular form
- Voronoi formula
References
{{Refbegin}}- {{Citation|last1=Bringmann|first1=Kathrin|author1-link=Kathrin Bringmann|last2=Folsom|first2=Amanda|author2-link=Amanda Folsom|doi=10.1515/crelle-2012-0102|journal=Journal für die Reine und Angewandte Mathematik|mr=3259042|pages=179–202|title=Almost harmonic Maass forms and Kac–Wakimoto characters|volume=694|year=2014}}
- {{Citation | last1=Bump | first1=Daniel | authorlink = Daniel Bump | title=Automorphic forms and representations | publisher=Cambridge University Press | series=Cambridge Studies in Advanced Mathematics | isbn=978-0-521-55098-7 |mr=1431508 | year=1997 | volume=55 | doi=10.1017/CBO9780511609572}}
- Anton Deitmar: Automorphe Formen. Springer, Berlin/ Heidelberg u. a. 2010, {{ISBN|978-3-642-12389-4}}.
- {{citation|last1=Duke|first1=W.|author1-link=William Duke (mathematician)|last2=Friedlander|first2=J. B.|author2-link=John Friedlander|last3=Iwaniec|first3=H.|author3-link=Henryk Iwaniec|doi=10.1007/s002220200223|issue=3|journal=Inventiones Mathematicae|mr=1923476|pages=489–577|title=The subconvexity problem for Artin {{mvar|L}}-functions|volume=149|year=2002}}
- Henryk Iwaniec : Spectral Methods of Automorphic Forms (Graduate Studies in Mathematics). American Mathematical Society; Auflage: 2. (November 2002), {{ISBN|978-0821831601}}.
- {{Citation | last1=Maass | first1=Hans | authorlink=Hans Maass|title=Über eine neue Art von nichtanalytischen automorphen Funktionen und die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen | doi=10.1007/BF01329622 |mr=0031519 | year=1949 | journal=Mathematische Annalen | volume=121 | pages=141–183}}
- 8 cubic meter-class dredger
- 8d
- 8-d
- 8 Days (disambiguation)
- 8dayz
- 8 December 2009 Baghdad bombings
- 8-demicube honeycomb
- 8 de Octubre Avenue
- 8-Dice cloth
- 8-dimensional polytope
- (8E)-9-((1E,3E)-nona-1,3-dien-1-yloxy)non-8-enoate synthase
- 8-epicedrol synthase
- 8-Eyed Spy
- 8 Eye's
- 8-face
- 8 February Revolution
- 8 FF
- 8 Flavahz
- 8 Flight Army Air Corps
- 8" floppy
- 8" floppy disk
- 8" floppy drive
- 8g
- 8-g
- 8-G