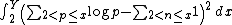“Maier's theorem”的意思、由来-开放百科全书

词条

Maier's theorem

释义

Proofs
References

In number theory, Maier's theorem {{harv|Maier|1985}} is a theorem about the numbers of primes in short intervals for which Cramér's probabilistic model of primes gives the wrong answer.

The theorem states that if π is the prime counting function and λ is greater than 1 then

does not have a limit as x tends to infinity; more precisely the lim sup is greater than 1, and the lim inf is less than 1. The Cramér model of primes predicts incorrectly that it has limit 1 when λ≥2 (using the Borel–Cantelli lemma).

Proofs

Maier proved his theorem using Buchstab's equivalent for the counting function of quasi-primes (set of numbers without prime factors lower to bound 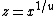, fixed). He also used an equivalent of the number of primes in arithmetic progressions of sufficient length due to Gallagher.

{{harvtxt|Pintz|2007}} gave another proof, and also showed that most probabilistic models of primes incorrectly predict the mean square error

of one version of the prime number theorem.

References

{{Citation | last1=Maier | first1=Helmut | author-link1=Helmut Maier | title=Primes in short intervals | url=http://projecteuclid.org/euclid.mmj/1029003189 | doi=10.1307/mmj/1029003189 | mr=783576 | year=1985 | journal=The Michigan Mathematical Journal | issn=0026-2285 | volume=32 | issue=2 | pages=221–225 | zbl=0569.10023 }}
{{Citation | authorlink=János Pintz | last1=Pintz | first1=János | title=Cramér vs. Cramér. On Cramér's probabilistic model for primes | url=http://projecteuclid.org/euclid.facm/1229619660 | mr=2363833 | year=2007 | journal= Functiones et Approximatio Commentarii Mathematici | volume=37 | pages=361–376 | zbl=1226.11096 | issn=0208-6573 | doi=10.7169/facm/1229619660}}
{{citation | last=Soundararajan | first=K. | authorlink=Kannan Soundararajan | chapter=The distribution of prime numbers | editor1-last=Granville | editor1-first=Andrew | editor1-link=Andrew Granville | editor2-last=Rudnick | editor2-first=Zeév | title=Equidistribution in number theory, an introduction. Proceedings of the NATO Advanced Study Institute on equidistribution in number theory, Montréal, Canada, July 11--22, 2005 | location=Dordrecht |publisher=Springer-Verlag | series=NATO Science Series II: Mathematics, Physics and Chemistry | volume=237 | pages=59–83 | year=2007 | isbn=978-1-4020-5403-7 | zbl=1141.11043 }}

3 : Theorems in analytic number theory|Probabilistic models|Theorems about prime numbers

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。