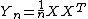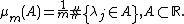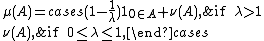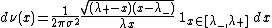“Marchenko–Pastur distribution”的意思、由来-开放百科全书

词条

Marchenko–Pastur distribution

释义

See also
References

In the mathematical theory of random matrices, the Marchenko–Pastur distribution, or Marchenko–Pastur law, describes the asymptotic behavior of singular values of large rectangular random matrices. The theorem is named after Ukrainian mathematicians Vladimir Marchenko and Leonid Pastur who proved this result in 1967.

If 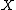denotes a random matrix whose entries are independent identically distributed random variables with mean 0 and variance 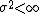, let

and let 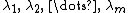be the eigenvalues of 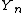(viewed as random variables). Finally, consider the random measure

Theorem. Assume that 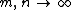so that the ratio 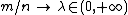. Then 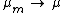(in weak* topology in distribution), where

and

with

The Marchenko–Pastur law also arises as the free Poisson law in free probability theory, having rate 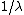and jump size .

References

{{cite journal |last=Götze |first=F. |last2=Tikhomirov |first2=A. |year=2004 |title=Rate of convergence in probability to the Marchenko–Pastur law |journal=Bernoulli |volume=10 |issue=3 |pages=503–548 |doi=10.3150/bj/1089206408 }}
{{cite journal |last=Marchenko |first=V. A. |last2=Pastur |first2=L. A. |year=1967 |title=Распределение собственных значений в некоторых ансамблях случайных матриц |trans-title=Distribution of eigenvalues for some sets of random matrices |language=ru |journal=Mat. Sb. |series=N.S. |volume=72 |issue=114:4 |pages=507–536 |doi=10.1070/SM1967v001n04ABEH001994 }} Link to free-access pdf of Russian version
{{cite book |last=Nica |first=A. |authorlink2=Roland Speicher |last2=Speicher |first2=R. |year=2006 |title=Lectures on the Combinatorics of Free probability theory |publisher=Cambridge Univ. Press |isbn=0-521-85852-6 |pages=204, 368 }} Link to free download [https://www.google.com/search?tbs=bks:1&q=isbn:0521858526 Another free access site]

2 : Probability distributions|Random matrices

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

See also

References