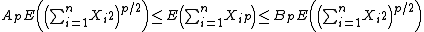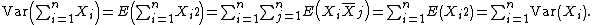- Statement of the inequality
- The second-order case
- See also
- Notes
In mathematics, the Marcinkiewicz–Zygmund inequality, named after Józef Marcinkiewicz and Antoni Zygmund, gives relations between moments of a collection of independent random variables. It is a generalization of the rule for the sum of variances of independent random variables to moments of arbitrary order. It is a special case of the Burkholder-Davis-Gundy inequality in the case of discrete-time martingales.
Statement of the inequality
Theorem [1][2] If  ,
, 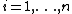 , are independent random variables such that
, are independent random variables such that 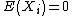 and
and 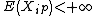 ,
, 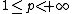 , then
, then
where 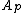 and
and 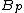 are positive constants, which depend only on
are positive constants, which depend only on 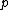 and not on the underlying distribution of the random variables involved.
and not on the underlying distribution of the random variables involved.
The second-order case
In the case 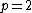 , the inequality holds with
, the inequality holds with 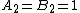 , and it reduces to the rule for the sum of variances of independent random variables with zero mean, known from elementary statistics: If
, and it reduces to the rule for the sum of variances of independent random variables with zero mean, known from elementary statistics: If 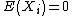 and
and 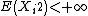 , then
, then
See also
Several similar moment inequalities are known as Khintchine inequality and Rosenthal inequalities, and there are also extensions to more general symmetric statistics of independent random variables.[3]
Notes
2. ^Yuan Shih Chow and Henry Teicher. Probability theory. Independence, interchangeability, martingales. Springer-Verlag, New York, second edition, 1988.
3. ^R. Ibragimov and Sh. Sharakhmetov. Analogues of Khintchine, Marcinkiewicz–Zygmund and Rosenthal inequalities for symmetric statistics. Scandinavian Journal of Statistics, 26(4):621–633, 1999.
- Jack And the Beanstalk
- Jack and The Beanstalk
- Jack and the Beanstalk (1902 film)
- Jack and the Beanstalk (1931 cartoon)
- Jack and the Beanstalk (1974 film)
- Jack and the Beanstalk (anime)
- Jack and the Beanstalk (film)
- Jack and the Cuckoo Clock Heart
- Jack and the Cuckoo-Clock Heart
- Jack and Triumph
- Jack and Triumph Show
- Jack And White
- Jack and White
- Jack Angus
- Jack Angus (disambiguation)
- Jack Angus (footballer)
- Jack Angus (footballer born 1909)
- Jackanory Playhouse
- Jack Anthony (wrestler)
- Jack Antonoff
- Jack Anwin
- Jack A. Quinn
- Jack Arbrew
- Jack Arena
- Jack arena