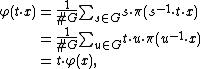1. Formulations
     Group-theoretic    Module-theoretic    Category-theoretic  

2. Proofs
     Module-theoretic  

3. Converse statement

4. Notes

5. References

In mathematics, Maschke's theorem,^[1][2] named after Heinrich Maschke,^[3] is a theorem in group representation theory that concerns the decomposition of representations of a finite group into irreducible pieces. Maschke's theorem allow one to make general conclusions about representations of a finite group G without actually computing them. It reduces the task of classifying all representations to a more manageable task of classifying irreducible representations, since when the theorem applies, any representation is a direct sum of irreducible pieces (constituents). Moreover, it follows from the Jordan–Hölder theorem that, while the decomposition into a direct sum of irreducible subrepresentations may not be unique, the irreducible pieces have well-defined multiplicities. In particular, a representation of a finite group over a field of characteristic zero is determined up to isomorphism by its character.

Formulations

Maschke's theorem addresses the question: when is a general (finite-dimensional) representation built from irreducible subrepresentations using the direct sum operation? This question (and its answer) are formulated differently for different perspectives on group representation theory.

Group-theoretic

Maschke's theorem is commonly formulated as a corollary to the following result:

Theorem. If {{var|V}} is a complex representation of a group {{var|G}} with a subrepresentation {{var|W}}, then there is another subrepresentation {{var|U}} of {{var|V}} such that {{var|V}}={{var|W}}⊕{{var|U}}.{{sfn|Fulton|Harris|loc=Proposition 1.5}}{{sfn|Serre|loc=Theorem 1}}

Then the corollary is

Corollary (Maschke's theorem). Every representation of a group {{var|G}} over a field {{var|F}} with characteristic not dividing the order of {{var|G}} is a direct sum of irreducible representations.{{sfn|Fulton|Harris|loc=Corollary 1.6}}{{sfn|Serre|loc=Theorem 2}}

The vector space of complex-valued class functions of a group {{var|G}} has a natural {{var|G}}-invariant inner product structure, described in the article Schur orthogonality relations. Maschke's theorem was originally proved for the case of representations over 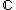by constructing {{var|U}} as the orthogonal complement of {{var|W}} under this inner product.

Module-theoretic

One of the approaches to representations of finite groups is through module theory. Representations of a group G are replaced by modules over its group algebra K[G] (to be precise, there is an isomorphism of categories between K[G]-Mod and Rep_G, the category of representations of G). Irreducible representations correspond to simple modules. In the module-theoretic language, Maschke's theorem asks: is an arbitrary module semisimple? In this context, the theorem can be reformulated as follows:

Maschke's Theorem. Let G be a finite group and K a field whose characteristic does not divide the order of G. Then K[G], the group algebra of G, is semisimple.^[4][5]

The importance of this result stems from the well developed theory of semisimple rings, in particular, the Artin–Wedderburn theorem (sometimes referred to as Wedderburn's Structure Theorem). When K is the field of complex numbers, this shows that the algebra K[G] is a product of several copies of complex matrix algebras, one for each irreducible representation.^[6] If the field K has characteristic zero, but is not algebraically closed, for example, K is a field of real or rational numbers, then a somewhat more complicated statement holds: the group algebra K[G] is a product of matrix algebras over division rings over K. The summands correspond to irreducible representations of G over K.^[7]

Category-theoretic

Reformulated in the language of semi-simple categories, Maschke's theorem states

Maschke's theorem. If {{var|G}} is a group and {{var|F}} is a field with characteristic not dividing the order of {{var|G}}, then the category of representations of {{var|G}} over {{var|F}} is semi-simple.

Proofs

Module-theoretic

Let V be a K[G]-submodule. We will prove that V is a direct summand. Let π be any K-linear projection of K[G] onto V. Consider

the map 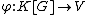given by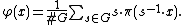

Then φ is again a projection: it is clearly K-linear, maps K[G] onto V, and induces the identity on V. Moreover we have

so φ is in fact K[G]-linear. By the splitting lemma, 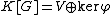. This proves that every submodule is a direct summand, that is, K[G] is semisimple.

Converse statement

The above proof depends on the fact that #G is invertible in K. This might lead one to ask if the converse of Maschke's theorem also holds: if the characteristic of K divides the order of G, does it follow that K[G] is not semisimple? The answer is yes.{{sfn|Serre|loc=Exercise 6.1}}

Proof. For 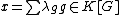define 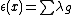. Let 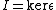. Then I is a K[G]-submodule. We will prove that for every nontrivial submodule V of K[G], 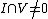. Let V be given, and let 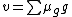be any nonzero element of V. If 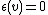, the claim is immediate. Otherwise, let 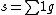. Then 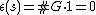so and 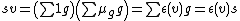so that 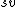is an element of both I and V. This proves that V is not a direct complement of I for all V, so K[G] is not semisimple.

Notes

References

• {{cite book

• {{cite book

• {{Fulton-Harris}}

• Payne v Cave
• Payne v. Cave
• Payneville, Kentucky
• Payne, Virginia
• Payne v. Tennessee
• Paynimism
• Paynimry
• Pay 'N Pak
• Payns
• Pay'n Takit
• Paynton
• Paynton Ferry
• Payntonian
• Payo de ojeda
• Payo Enríquez de Rivera Manrique
• Pay-off
• Payoff (disambiguation)
• Pay off your mortgage in two years
• Payogasta
• Payola$
• Pay*ola (band)
• Payola (New Zealand band)
• Payola Scandal
• Pay on production
• Payoomkawichum