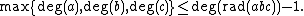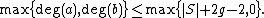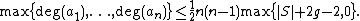1. Examples

2. Proof

3. Generalizations

4. References

5. External links

The Mason–Stothers theorem, or simply Mason's theorem, is a mathematical theorem about polynomials, analogous to the abc conjecture for integers. It is named after {{Interlanguage link multi|W. Wilson Stothers|nl|3=Walter Wilson Stothers}}, who published it in 1981,^[1] and R. C. Mason, who rediscovered it shortly thereafter.^[2]

The theorem states:

Let {{math|a(t)}}, {{math|b(t)}}, and {{math|c(t)}} be relatively prime polynomials over a field such that {{math|1=a + b = c}} and such that not all of them have vanishing derivative. Then

Here {{math|rad(f)}} is the product of the distinct irreducible factors of {{mvar|f}}. For algebraically closed fields it is the polynomial of minimum degree that has the same roots as {{mvar|f}}; in this case {{math|deg(rad(f))}} gives the number of distinct roots of {{mvar|f}}.^[3]

Examples

• Over fields of characteristic 0 the condition that {{mvar|a}}, {{mvar|b}}, and {{mvar|c}} do not all have vanishing derivative is equivalent to the condition that they are not all constant. Over fields of characteristic {{math|p > 0}} it is not enough to assume that they are not all constant. For example, the identity {{math|1=t^p + 1 = (t + 1)^p}} gives an example where the maximum degree of the three polynomials ({{mvar|a}} and {{mvar|b}} as the summands on the left hand side, and {{mvar|c}} as the right hand side) is {{mvar|p}}, but the degree of the radical is only {{math|2}}.
• Taking {{math|1=a(t) = tⁿ}} and {{math|1=c(t) = (t+1)ⁿ}} gives an example where equality holds in the Mason–Stothers theorem, showing that the inequality is in some sense the best possible.
• A corollary of the Mason–Stothers theorem is the analog of Fermat's last theorem for function fields: if {{math|1= a(t)ⁿ + b(t)ⁿ = c(t)ⁿ}} for {{mvar|a}}, {{mvar|b}}, {{mvar|c}} relatively prime polynomials over a field of characteristic not dividing {{mvar|n}} and {{math|n > 2}} then either at least one of {{mvar|a}}, {{mvar|b}}, or {{mvar|c}} is 0 or they are all constant.

Proof

Step 1. The condition {{math|1=a + b + c = 0}} implies that the Wronskians {{math|1=W(a, b) = ab′ − a′b}}, {{math|W(b, c)}}, and {{math|W(c, a)}} are all equal. Write {{mvar|W}} for their common value.

Step 2. The condition that at least one of the derivatives {{math|a′}}, {{math|b′}}, or {{math|c′}} is nonzero and that {{mvar|a}}, {{mvar|b}}, and {{mvar|c}} are coprime is used to show that {{mvar|W}} is nonzero.

For example, if {{math|1=W = 0}} then {{math|1=ab′ = a′b}} so {{mvar|a}} divides {{math|a′}} (as {{mvar|a}} and {{mvar|b}} are coprime) so {{math|1=a′ = 0}} (as {{math|deg a > deg a′}} unless {{mvar|a}} is constant).

Step 3. {{mvar|W}} is divisible by each of the greatest common divisors {{math|(a, a′)}}, {{math|(b, b′)}}, and {{math|(c, c′)}}. Since these are coprime it is divisible by their product, and since {{mvar|W}} is nonzero we get

{{math|deg (a, a′) + deg (b, b′) + deg (c, c′) ≤ deg W.}}

Step 4. Substituting in the inequalities

{{math|deg (a, a′) ≥ deg a}} − (number of distinct roots of {{mvar|a}})

{{math|deg (b, b′) ≥ deg b}} − (number of distinct roots of {{mvar|b}})

{{math|deg (c, c′) ≥ deg c}} − (number of distinct roots of {{mvar|c}})

(where the roots are taken in some algebraic closure) and

{{math|deg W ≤ deg a + deg b − 1 }}

we find that

{{math|deg c ≤ (number of distinct roots of abc) − 1}}

which is what we needed to prove.

Generalizations

There is a natural generalization in which the ring of polynomials is replaced by a one-dimensional function field.

Let {{mvar|k}} be an algebraically closed field of characteristic 0, let {{math|C/k}} be a smooth projective curve

of genus {{mvar|g}}, let

be rational functions on {{mvar|C}} satisfying ,

and let

Then

Here the degree of a function in {{math|k(C)}} is the degree of

the map it induces from {{mvar|C}} to P¹.

This was proved by Mason, with an alternative short proof published the same year by J. H. Silverman

.^[5]

There is a further generalization, due independently to J. F. Voloch^[6]

and to

that gives an upper bound for {{mvar|n}}-variable {{mvar|S}}-unit

equations {{math|1=a₁ + a₂ + ... + a_n = 1}} provided that

no subset of the {{math|a_i}} are {{mvar|k}}-linearly dependent. Under this assumption, they prove that

References

External links

• {{mathworld|urlname=MasonsTheorem|title=Mason's Theorem}}
• Mason-Stothers Theorem and the ABC Conjecture, Vishal Lama. A cleaned-up version of the proof from Lang's book.

• Under water predation
• Underwater Pyramids
• Underwater ray romano
• Underwater respiration
• Underwater rifle
• Underwater Rugby
• Underwater rugby in Colombia
• Underwater rugby in the United States
• Underwater rugby in USA
• Underwater search and recovery
• Underwater sports
• Underwater Sun
• Underwater swimming (disambiguation)
• Underwater telephone
• Underwater tunnel
• Underwater volcano (disambiguation)
• Underwater weighing
• Under Water World
• Underwater World (disambiguation)
• Underwater world guam
• Underwater World Guam
• UnderWater World Guam
• Underwater World (Hanoi Rocks song)
• Underwater World (song)
• Underwear as outerwear