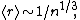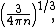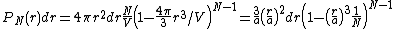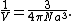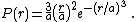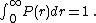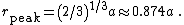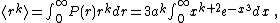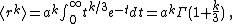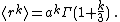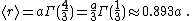“Mean inter-particle distance”的意思、由来-开放百科全书

词条

Mean inter-particle distance

释义

Ambiguity
Ideal gas
Nearest neighbor distribution Mean distance and higher NN distribution moments
References
See also

Mean inter-particle distance (or mean inter-particle separation) is the mean distance between microscopic particles (usually atoms or molecules) in a macroscopic body.

Ambiguity

From the very general considerations, the mean inter-particle distance is proportional to the size of the per-particle volume , i.e.,

where 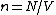is the particle density. However, barring a few simple cases such as the ideal gas model, precise calculations of the proportionality factor are impossible analytically. Therefore, approximate expressions are often used. One such an estimation is the Wigner-Seitz radius

which corresponds to the radius of a sphere having per-particle volume . Another popular definition is

,

corresponding to the length of the edge of the cube with the per-particle volume . The two definitions differ by a factor of approximately 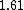, so one has to exercise care if an article fails to define the parameter exactly. On the other hand, it is often used in qualitative statements where such a numeric factor is either irrelevant or plays an insignificant role, e.g.,

"a potential energy ... is proportional to some power n of the inter-particle distance r" (Virial theorem)
"the inter-particle distance is much larger than the thermal de Broglie wavelength" (Kinetic theory)

Ideal gas

Nearest neighbor distribution

We want to calculate probability distribution function of distance to the nearest neighbor (NN) particle. (The problem was first considered by Paul Hertz;^[1] for a modern derivation see, e.g.,.^[2]) Let us assume particles inside a sphere having volume , so that 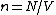. Note that since the particles in the ideal gas are non-interacting, the probability to find a particle at a certain distance from another particle is the same as probability to find a particle at the same distance from any other point; we shall use the center of the sphere.

An NN particle at distance means exactly one of the particles resides at that distance while the rest

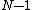particles are at larger distances, i.e., they are somewhere outside the sphere with radius .

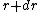The probability to find a particle at the distance from the origin between and is

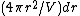, plus we have kinds of way to choose which particle , while the probability to find a particle outside that sphere is 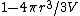. The sought-for expression is then

where we substituted

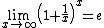Note that is the Wigner-Seitz radius. Finally, taking the limit and using , we obtain

One can immediately check that

The distribution peaks at

Mean distance and higher NN distribution moments

or, using the 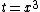substitution,

where is the gamma function. Thus,

In particular,

References

1. ^{{Cite journal| doi = 10.1007/BF01450410| issn = 0025-5831| volume = 67| issue = 3| pages = 387–398| last = Hertz| first = Paul| title = Über den gegenseitigen durchschnittlichen Abstand von Punkten, die mit bekannter mittlerer Dichte im Raume angeordnet sind| journal = Mathematische Annalen| accessdate = 2011-03-03| year = 1909| url = http://www.springerlink.com/content/q133104qq7596l37/}}
2. ^{{Cite journal| doi = 10.1103/RevModPhys.15.1| volume = 15| issue = 1| pages = 1| last = Chandrasekhar| first = S.| title = Stochastic Problems in Physics and Astronomy| journal = Reviews of Modern Physics| accessdate = 2011-03-01| date = 1943-01-01| url = http://link.aps.org/doi/10.1103/RevModPhys.15.1| bibcode=1943RvMP...15....1C}}

Ambiguity

Ideal gas

Nearest neighbor distribution

Mean distance and higher NN distribution moments

References

See also