- Related hyperbolic tiling
- See also
- References
- External links
In geometry, the medial rhombic triacontahedron is a nonconvex isohedral polyhedron. It is a stellation of the rhombic triacontahedron, and can also be called small stellated triacontahedron. Its dual is the dodecadodecahedron.
Its 24 vertices are all on the 12 axes with 5-fold symmetry (i.e. each corresponds to one of the 12 vertices of the icosahedron). This means that on each axis there is an inner and an outer vertex. The ratio of outer to inner vertex radius is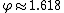 
, the golden ratio.
It has 30 intersecting rhombic faces, which correspond to the faces of the convex rhombic triacontahedron. The diagonals in the rhombs of the convex solid have a ratio of 1 to 
. The medial solid can be generated from the convex one by stretching the shorter diagonal from length 1 to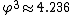 
. So the ratio of rhomb diagonals in the medial solid is 1 to 
.
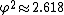This solid is to the compound of small stellated dodecahedron and great dodecahedron what the convex one is to the compound of dodecahedron and icosahedron:
The crossing edges in the dual compound are the diagonals of the rhombs.
| total_width = 500 | image1 = Rhombic triacontahedron 1 (convex), size m (crop matching medial), pyritohedral.png | image2 = Rhombic triacontahedron 2 (medial), size m (crop), pyritohedral.png | image3 = Skeleton pair Gr12 and dual, size m (crop), thick.png | footer = Convex and medial rhombic triacontahedron (both shown with pyritohedral symmetry) and on the right the dual compound of Kepler–Poinsot solids }}{{multiple image | total_width = 500 | image1 = Rhombic triacontahedron 2 (medial), size m, 2-fold.png | image2 = Rhombic triacontahedron 2 (medial), size m, 3-fold.png | image3 = Rhombic triacontahedron 2 (medial), size m, 5-fold.png | footer = Orthographic projections from 2-, 3- and 5-fold symmetry axes }} |
Related hyperbolic tiling
It is topologically equivalent to a quotient space of the hyperbolic order-5 square tiling, by distorting the rhombi into squares. As such, it is topologically a regular polyhedron of index two:[1]
Note that the order-5 square tiling is dual to the order-4 pentagonal tiling, and a quotient space of the order-4 pentagonal tiling is topologically equivalent to the dual of the medial rhombic triacontahedron, the dodecadodecahedron.
See also
- Great rhombic triacontahedron
- Great triambic icosahedron
References
- {{Citation | last1=Wenninger | first1=Magnus | author1-link=Magnus Wenninger | title=Dual Models | publisher=Cambridge University Press | isbn=978-0-521-54325-5 | mr= 730208| year=1983}}
External links
- {{mathworld | urlname = MedialRhombicTriacontahedron| title =Medial Rhombic Triacontahedron}}
- David I. McCooey: animation and measurements
- Uniform polyhedra and duals
- Sasanian reconquest of Yemen
- Sasanid dynasty
- Sasanid Empire
- Sasa nipponica
- Sasano
- Sasanoa River
- Sasa Novakovic
- Sasanqua camellia
- Sasan Sara
- Sasan Ultra Mega Power Project
- Sasanuma
- Sasa Plus 88
- Sasa Popin
- Sasar
- Sasa Racha
- Sasa Radulovic
- Sasa Radulovic (economist)
- Sasaram back-to-back HVDC converter station
- Sasa Rankovic
- Sasar language
- Sasarm
- Sasaru-Enwan Igwe language
- Sasaru-Enwan-Igwe language
- Sasaru language
- S. A. Saryg-Ool