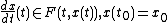- Applications
- Generalizations
- See also
- References
- Further reading
In functional analysis, a branch of mathematics, the most popular version of the Michael selection theorem, named after Ernest Michael, states the following:
Let E be a Banach space, X a paracompact space anda lower hemicontinuous multivalued map with nonempty convex closed values. Then there exists a continuous selection
of F.
Conversely, if any lower semicontinuous multimap from topological space X to a Banach space, with nonempty convex closed values admits continuous selection, then X is paracompact. This provides another characterization for paracompactness.
Applications
Michael selection theorem can be applied to show that the differential inclusion
has a C1 solution when F is lower semi-continuous and F(t, x) is a nonempty closed and convex set for all (t, x). When F is single valued, this is the classic Peano existence theorem.
Generalizations
A theorem due to Deutsch and Kenderov generalizes Michel selection theorem to an equivalence relating approximate selections to almost lower hemicontinuity, where 
is said to be almost lower hemicontinuous if at each 
, all neighborhoods 
of 
there exists a neighborhood 
of 
such that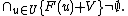 
Precisely, Deutsch–Kenderov theorem states that if 
is paracompact, 
a normed vector space and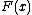 
is nonempty convex for each , then is almost lower hemicontinuous if and only if has continuous approximate selections, that is, for each neighborhood of in there is a continuous function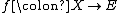 
such that for each , 
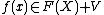.[1]
In a note Xu proved that Deutsch–Kenderov theorem is also valid if is a locally convex topological vector space.[2]
See also
- Zero-dimensional Michael selection theorem
- List of selection theorems
References
2. ^{{cite journal|last1=Xu|first1=Yuguang|title=A Note on a Continuous Approximate Selection Theorem|journal=Journal of Approximation Theory|date=December 2001|volume=113|issue=2|pages=324–325|doi=10.1006/jath.2001.3622}}
Further reading
- {{Cite journal | last1=Michael | first1=Ernest | author1-link=Ernest Michael | title=Continuous selections. I |mr=0077107 | year=1956 | journal=Annals of Mathematics |series=Second Series | volume=63 | pages=361–382 | issue=2 | jstor=1969615 | doi=10.2307/1969615}}
- {{cite book |first1=Dušan |last1=Repovš |author1-link=Dušan Repovš|first2=Pavel V. |last2=Semenov |chapter=Continuous Selections of Multivalued Mappings |editor1-last=Hart |editor1-first=K. P. |editor2-last=van Mill |editor2-first=J. |editor3-last=Simon |editor3-first=P. |title=Recent Progress in General Topology |volume=III |year=2014 |publisher=Springer |location=Berlin |isbn=978-94-6239-023-2 |pages=711–749 |arxiv=1401.2257 |bibcode=2014arXiv1401.2257R }}
- {{cite book |first=Jean-Pierre |last=Aubin |first2=Arrigo |last2=Cellina |title=Differential Inclusions, Set-Valued Maps And Viability Theory |series=Grundl. der Math. Wiss. |volume=264 |publisher=Springer-Verlag |location=Berlin |year=1984 |isbn=3-540-13105-1 }}
- {{cite book |first=Jean-Pierre |last=Aubin |first2=H. |last2=Frankowska |author2-link=Hélène Frankowska|title=Set-Valued Analysis |publisher=Birkhäuser |location=Basel |year=1990 |isbn=3-7643-3478-9 }}
- {{cite book |first=Klaus |last=Deimling |title=Multivalued Differential Equations |publisher=Walter de Gruyter |year=1992 |isbn=3-11-013212-5 }}
- {{cite book |first1=Dušan |last1=Repovš |author1-link=Dušan Repovš |first2=Pavel V. |last2=Semenov |title=Continuous Selections of Multivalued Mappings |publisher=Kluwer Academic Publishers |location=Dordrecht |year=1998 |isbn=0-7923-5277-7 }}
- {{cite journal |first1=Dušan |last1=Repovš |author1-link=Dušan Repovš|first2=Pavel V. |last2=Semenov |title=Ernest Michael and Theory of Continuous Selections |journal=Topology and its Applications |volume=155 |issue=8 |year=2008 |pages=755–763 |doi=10.1016/j.topol.2006.06.011 }}
- {{cite book |last=Aliprantis |first=Charalambos D. |first2=Kim C. |last2=Border |title=Infinite Dimensional Analysis : Hitchhiker's Guide |location= |publisher=Springer |edition=3rd |year=2007 |isbn=978-3-540-32696-0 }}
- {{cite book |first=S. |last=Hu |first2=N. |last2=Papageorgiou |title=Handbook of Multivalued Analysis |volume=Vol. I |publisher=Kluwer |isbn=0-7923-4682-3 }}
- Antiterra
- Anti-terrorism
- Anti-Terrorism and Effective Death Penalty Act
- Antiterrorism and Effective Death Penalty Act
- Antiterrorism and Effective Death Penalty Act of 1996
- Anti-Terrorism, Crime and Security Act 2001
- Anti-Terrorism Crime and Security Act 2001
- Anti-terrorism, Crime and Security Act 2001
- Anti-terrorist
- Anti-terrorist Branch
- Anti terrorist policies of the metropolitan police
- Anti-terrorist policies of the Metropolitan police
- Anti-theft system
- Antitheism
- Antitheist
- Antitheses
- Antithesis
- Antithrombin
- Antithrombin deficiency, congenital
- Antithrombin III
- Anti-thymocyte globulin
- Anti tom fiction
- Anti tom literature
- Anti-Tom literature
- Anti tom novel