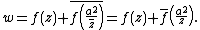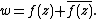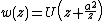- Example
- See also
- References
- External links
In fluid dynamics the Milne-Thomson circle theorem or the circle theorem is a statement giving a new stream function for a fluid flow when a cylinder is placed into that flow.[1][2] It was named after the English mathematician L. M. Milne-Thomson.
Let 
be the complex potential for a fluid flow, where all singularities of lie in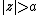 
. If a circle 
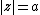is placed into that flow, the complex potential for the new flow is given by[3]
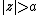with same singularities as in and 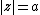is a streamline. On the circle , 
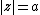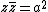, therefore
Example
Consider a uniform irrotational flow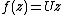 
with velocity 
flowing in the positive 
direction and place an infinitely long cylinder of radius 
in the flow with the center of the cylinder at the origin. Then 
, hence using circle theorem,
represents the complex potential of uniform flow over a cylinder.
See also
- Potential flow
- Conformal mapping
- Velocity potential
- Milne-Thomson method for finding a holomorphic function
References
2. ^{{cite book|last=Raisinghania|first=M.D.|title=Fluid Dynamics|url=https://books.google.com/books?id=wq3TU5tArTkC&lpg=PA211&ots=yThvgwi8Rv&dq=milne%20thomson%20circle%20theorem&pg=PA211#v=onepage&q=milne%20thomson%20circle%20theorem&f=false}}
3. ^{{cite thesis|last=Tulu|first=Serdar|title=Vortex dynamics in domains with boundaries|url=http://library.iyte.edu.tr/tezler/doktora/matematik/T000958.pdf|year=2011}}
External links
- Răstolţu-Deşert
- Răstolţu Deşert
- Răstolț
- Răstolțu Deșert
- Răsurile
- Rătei River (Dâmboviţa)
- Rătei River (Ialomiţa)
- Rătez
- Răteşti
- Răteşti Monastery
- Rătăşel River
- Răuceşti
- Răutu
- Răutăciosul adolescent
- Răuţel
- Răuţeni
- Răuțeni
- Răvaşu River
- Răvăşel
- Răvășel
- Războieni Cetate
- Războieni-Cetate
- Războienii
- Războieni, Neamţ
- Răzbuneni