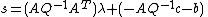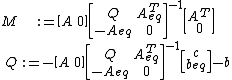- Formulation
- Convex quadratic-minimization: Minimum conditions
- See also
- Notes
- References
- Further reading
- External links
In mathematical optimization theory, the linear complementarity problem (LCP) arises frequently in computational mechanics and encompasses the well-known quadratic programming as a special case. It was proposed by Cottle and Dantzig {{nowrap|in 1968.[1][2][1]}}
Formulation
Given a real matrix M and vector q, the linear complementarity problem LCP(M, q) seeks vectors z and w which satisfy the following constraints:
-
 (that is, each component of these two vectors is non-negative)
(that is, each component of these two vectors is non-negative) -
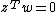 or equivalently
or equivalently  This is the complementarity condition, since it implies that, for all
This is the complementarity condition, since it implies that, for all 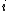 , at most one of
, at most one of  and
and  can be positive.
can be positive. -
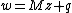
A sufficient condition for existence and uniqueness of a solution to this problem is that M be symmetric positive-definite. If M is such that {{math|LCP(M, q)}} have a solution for every q, then M is a Q-matrix. If M is such that {{math|LCP(M, q)}} have a unique solution for every q, then M is a P-matrix. Both of these characterizations are sufficient and necessary.[2]
The vector w is a slack variable,[3] and so is generally discarded after z is found. As such, the problem can also be formulated as:
-

-
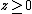
-
 (the complementarity condition)
(the complementarity condition)
Convex quadratic-minimization: Minimum conditions
Finding a solution to the linear complementarity problem is associated with minimizing the quadratic function
subject to the constraints
These constraints ensure that f is always non-negative. The minimum of f is 0 at z if and only if z solves the linear complementarity problem.
If M is positive definite, any algorithm for solving (strictly) convex QPs can solve the LCP. Specially designed basis-exchange pivoting algorithms, such as Lemke's algorithm and a variant of the simplex algorithm of Dantzig have been used for decades. Besides having polynomial time complexity, interior-point methods are also effective in practice.
Also, a quadratic-programming problem stated as minimize 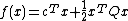 subject to
subject to  as well as
as well as  with Q symmetric
with Q symmetric
is the same as solving the LCP with
This is because the Karush–Kuhn–Tucker conditions of the QP problem can be written as:
with v the Lagrange multipliers on the non-negativity constraints, λ the multipliers on the inequality constraints, and s the slack variables for the inequality constraints. The fourth condition derives from the complementarity of each group of variables {{math|(x, s)}} with its set of KKT vectors (optimal Lagrange multipliers) being {{math|(v, λ)}}. In that case,
If the non-negativity constraint on the x is relaxed, the dimensionality of the LCP problem can be reduced to the number of the inequalities, as long as Q is non-singular (which is guaranteed if it is positive definite). The multipliers v are no longer present, and the first KKT conditions can be rewritten as:
or:
pre-multiplying the two sides by A and subtracting b we obtain:
The left side, due to the second KKT condition, is s. Substituting and reordering:
Calling now
we have an LCP, due to the relation of complementarity between the slack variables s and their Lagrange multipliers λ. Once we solve it, we may obtain the value of x from λ through the first KKT condition.
Finally, it is also possible to handle additional equality constraints:
This introduces a vector of Lagrange multipliers μ, with the same dimension as  .
.
It is easy to verify that the M and Q for the LCP system 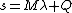 are now expressed as:
are now expressed as:
From λ we can now recover the values of both x and the Lagrange multiplier of equalities μ:
In fact, most QP solvers work on the LCP formulation, including the interior point method, principal / complementarity pivoting, and active set methods.[4][5] LCP problems can be solved also by the criss-cross algorithm,[6][7][8][9] conversely, for linear complementarity problems, the criss-cross algorithm terminates finitely only if the matrix is a sufficient matrix.[8][9] A sufficient matrix is a generalization both of a positive-definite matrix and of a P-matrix, whose principal minors are each positive.[8][9][10]
Such LCPs can be solved when they are formulated abstractly using oriented-matroid theory.[11][12][13]
See also
- Complementarity theory
- Physics engine Impulse/constraint type physics engines for games use this approach.
- Contact dynamics Contact dynamics with the nonsmooth approach.
- Bimatrix games can be reduced to a LCP.
Notes
2. ^{{cite journal|last1=Murty|first1=Katta G.|title=On the number of solutions to the complementarity problem and spanning properties of complementary cones|journal=Linear Algebra and its Applications|date=January 1972|volume=5|issue=1|pages=65–108|doi=10.1016/0024-3795(72)90019-5}}
3. ^{{citation|title=Convex Optimization of Power Systems|first=Joshua Adam|last=Taylor|publisher=Cambridge University Press|year=2015| isbn=9781107076877|page=172|url=https://books.google.com/books?id=JBdoBgAAQBAJ&pg=PA172}}.
4. ^1 {{harvtxt|Murty|1988}}
5. ^1 {{harvtxt|Cottle|Pang|Stone|1992}}
6. ^{{harvtxt|Fukuda|Namiki|1994}}
7. ^{{harvtxt|Fukuda|Terlaky|1997}}
8. ^1 2 {{cite journal|first1=D. |last1=den Hertog |first2=C.| last2=Roos |first3=T. |last3=Terlaky|title=The linear complementarity problem, sufficient matrices, and the criss-cross method|journal=Linear Algebra and its Applications|volume=187|date=1 July 1993|pages=1–14|url=http://core.ac.uk/download/pdf/6714737.pdf|doi=10.1016/0024-3795(93)90124-7}}
9. ^1 2 {{cite journal |first1=Zsolt |last1=Csizmadia |first2=Tibor |last2=Illés|title=New criss-cross type algorithms for linear complementarity problems with sufficient matrices|journal=Optimization Methods and Software| volume=21 |year=2006 |number=2 |pages=247–266|doi=10.1080/10556780500095009|url=http://www.cs.elte.hu/opres/orr/download/ORR03_1.pdf|}}
10. ^{{cite journal| last1=Cottle | first1=R. W. |authorlink1=Richard W. Cottle|last2=Pang|first2=J.-S.|last3=Venkateswaran|first3=V.|title=Sufficient matrices and the linear complementarity problem |journal=Linear Algebra and its Applications|volume=114–115|date=March–April 1989|pages=231–249|doi=10.1016/0024-3795(89)90463-1 |url=http://www.sciencedirect.com/science/article/pii/0024379589904631 |mr=986877|ref=harv}}
11. ^{{harvtxt|Todd|1985|}}
12. ^{{harvtxt|Terlaky|Zhang|1993}}: {{cite journal|last1=Terlaky|first1=Tamás||last2=Zhang|first2=Shu Zhong|title=Pivot rules for linear programming: A Survey on recent theoretical developments|series=Degeneracy in optimization problems|journal=Annals of Operations Research|volume=46–47|year=1993|issue=1|pages=203–233|doi=10.1007/BF02096264|mr=1260019|citeseerx=10.1.1.36.7658 |issn=0254-5330|ref=harv}}
13. ^{{cite book|last=Björner|first=Anders|last2=Las Vergnas|author2-link=Michel Las Vergnas|first2=Michel|last3=Sturmfels|first3=Bernd|authorlink3=Bernd Sturmfels|last4=White|first4=Neil|last5=Ziegler|first5=Günter|authorlink5=Günter M. Ziegler|title=Oriented Matroids|chapter=10 Linear programming|publisher=Cambridge University Press|year=1999|isbn=978-0-521-77750-6|chapter-url=http://ebooks.cambridge.org/ebook.jsf?bid=CBO9780511586507|pages=417–479|doi=10.1017/CBO9780511586507|mr=1744046}}
References
- {{cite book|last1=Cottle|first1=Richard W.|last2=Pang|first2=Jong-Shi|last3=Stone|first3=Richard E.|title=The linear complementarity problem | series=Computer Science and Scientific Computing|publisher=Academic Press, Inc.|location=Boston, MA|year=1992|pages=xxiv+762 pp|isbn=978-0-12-192350-1|mr=1150683|ref=harv}}
- {{cite journal|last1=Cottle|first1=R. W.|authorlink1=Richard W. Cottle|last2=Pang|first2=J.-S.|last3=Venkateswaran|first3=V.|title=Sufficient matrices and the linear complementarity problem|journal=Linear Algebra and its Applications|volume=114–115|date=March–April 1989|pages=231–249|doi=10.1016/0024-3795(89)90463-1| url=http://www.sciencedirect.com/science/article/pii/0024379589904631|mr=986877|ref=harv}}
- {{cite journal|first1=Zsolt|last1=Csizmadia|first2=Tibor|last2=Illés|title=New criss-cross type algorithms for linear complementarity problems with sufficient matrices|journal=Optimization Methods and Software|volume=21|year=2006|number=2|pages=247–266|doi=10.1080/10556780500095009|
url=http://www.cs.elte.hu/opres/orr/download/ORR03_1.pdf|}}
- {{cite journal|last1=Fukuda|first1=Komei|authorlink1=Komei Fukuda|last2=Namiki|first2=Makoto|title=On extremal behaviors of Murty's least index method|journal=Mathematical Programming|date=March 1994|pages=365–370|volume=64|issue=1|doi=10.1007/BF01582581|ref=harv|mr=1286455}}
- {{cite journal|first1=D. |last1=den Hertog|first2=C.|last2=Roos|first3=T.|last3=Terlaky|title=The linear complementarity problem, sufficient matrices, and the criss-cross method| journal=Linear Algebra and its Applications|volume=187|date=1 July 1993|pages=1–14|url=http://core.ac.uk/download/pdf/6714737.pdf|doi=10.1016/0024-3795(93)90124-7|ref=harv}}
- {{cite book|last=Murty|first=K. G.|title=Linear complementarity, linear and nonlinear programming|series=Sigma Series in Applied Mathematics|volume=3|publisher=Heldermann Verlag|location=Berlin|year=1988|pages=xlviii+629 pp|isbn=978-3-88538-403-8|url=http://ioe.engin.umich.edu/people/fac/books/murty/linear_complementarity_webbook/|mr=949214|id=Updated and free PDF version at Katta G. Murty's website|ref=harv|deadurl=yes|archiveurl=https://web.archive.org/web/20100401043940/http://ioe.engin.umich.edu/people/fac/books/murty/linear_complementarity_webbook/|archivedate=2010-04-01|df=}}
- {{cite journal|first1=Komei|last1=Fukuda||first2=Tamás|last2=Terlaky||title=Criss-cross methods: A fresh view on pivot algorithms|journal=Mathematical Programming, Series B|volume=79|issue=1–3| pages=369–395|series=Papers from the 16th International Symposium on Mathematical Programming held in Lausanne, 1997|editors=Thomas M. Liebling and Dominique de Werra|year=1997|doi=10.1007/BF02614325|mr=1464775|ref=harv|id=Postscript preprint|citeseerx=10.1.1.36.9373}}
- {{cite journal|last=Todd|first=Michael J.|authorlink=Michael J. Todd (mathematician)|title=Linear and quadratic programming in oriented matroids|journal=Journal of Combinatorial Theory|series=Series B|volume=39|year=1985|issue=2|pages=105–133|mr=811116|doi=10.1016/0095-8956(85)90042-5|ref=harv}}
- {{cite web | url=http://www.utdallas.edu/~chandra/documents/6311/bimatrix.pdf | title=Bimatrix games | accessdate=18 December 2015 | author=R. Chandrasekaran | pages=5–7}}
Further reading
- R. W. Cottle and G. B. Dantzig. Complementary pivot theory of mathematical programming. Linear Algebra and its Applications, 1:103-125, 1968.
- {{cite journal|last1=Terlaky|first1=Tamás||last2=Zhang|first2=Shu Zhong|title=Pivot rules for linear programming: A Survey on recent theoretical developments|series=Degeneracy in optimization problems|journal=Annals of Operations Research|volume=46–47|year=1993|issue=1|pages=203–233|doi=10.1007/BF02096264|mr=1260019|citeseerx=10.1.1.36.7658 |issn=0254-5330|ref=harv}}
External links
- [https://web.archive.org/web/20041029022008/http://www.american.edu/econ/gaussres/optimize/quadprog.src LCPSolve] — A simple procedure in GAUSS to solve a linear complementarity problem
- Siconos/Numerics open-source GPL implementation in C of Lemke's algorithm and other methods to solve LCPs and MLCPs
- Pterophyte
- Pteropodid
- Pteropodinae
- Pteropodocys
- Pteropterus
- Pteroptochos
- Pteroptochos castaneus
- Pteroptochos megapodius
- Pteroptochos tarnii
- Pteropus
- Pteropus admiralitatum
- Pteropus aldabrensis
- Pteropus alecto
- Pteropus anetianus
- Pteropus brunneus
- Pteropus caniceps
- Pteropus conspicillatus
- Pteropus dasymallus
- Pteropus faunulus
- Pteropus fundatus
- Pteropus giganteus
- Pteropus gilliardorum
- Pteropus griseus
- Pteropus howensis
- Pteropus hypomelanus