“Linear grammar”的意思、由来-开放百科全书

词条

Linear grammar

释义

Example
Relationship with regular grammars
Expressive power
Closure properties
References

In computer science, a linear grammar is a context-free grammar that has at most one nonterminal in the right hand side of each of its productions.

A linear language is a language generated by some linear grammar.

Example

A simple linear grammar is G with N = {S}, Σ = {a, b}, P with start symbol S and rules

S → aSb

S → ε

It generates the language .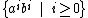

Relationship with regular grammars

Two special types of linear grammars are the following:

the left-linear or left regular grammars, in which all nonterminals in right hand sides are at the left ends;
the right-linear or right regular grammars, in which all nonterminals in right hand sides are at the right ends.

Collectively, these two special types of linear grammars are known as the regular grammars; both can describe exactly the regular languages.

Another special type of linear grammar is the following:

linear grammars in which all nonterminals in right hand sides are at the left or right ends, but not necessarily all at the same end.

By inserting new nonterminals, every linear grammar can be brought into this form without affecting the language generated.

For instance, the rules of G above can be replaced with

S → aA

A → Sb

S → ε

Hence, linear grammars of this special form can generate all linear languages.

Expressive power

All regular languages are linear; conversely, an example of a linear, non-regular language is {aⁿbⁿ}, as explained above.

All linear languages are context-free; conversely, an example of a context-free, non-linear language is the Dyck language of well-balanced bracket pairs.

Hence, the regular languages are a proper subset of the linear languages, which in turn are a proper subset of the context-free languages.

While the linear languages that are regular languages are deterministic, there exist linear languages that are nondeterministic. For example, the language of even-length palindromes on the alphabet of 0 and 1 has the linear grammar S → 0S0 | 1S1 | ε. An arbitrary string of this language cannot be parsed without reading all its letters first which means that a pushdown automaton has to try alternative state transitions to accommodate for the different possible lengths of a semi-parsed string.^[1] This language is nondeterministic. Since nondeterministic context-free languages cannot be accepted in linear time, linear languages cannot be accepted in linear time in the general case. Furthermore, it is undecidable whether a given context-free language is a linear context-free language.^[2]

Closure properties

If L is a linear language and M is a regular language, then the intersection 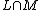is again a linear language; in other words, the linear languages are closed under intersection with regular sets. Furthermore, the linear languages are closed under homomorphism and inverse homomorphism.^[3] These three closure properties show that the linear languages form a full trio. Full trios in general are language families that enjoy a couple of other desirable mathematical properties.

References

1. ^{{cite book | last = Hopcroft | first = John |author2=Rajeev Motwani |author3=Jeffrey Ullman | title = Introduction to automata theory, languages, and computation 2nd edition | year = 2001 | publisher = Addison-Wesley | pages = 249–253 }}
2. ^{{cite journal | last=Greibach | first=Sheila | title=The Unsolvability of the Recognition of Linear Context-Free Languages |date=October 1966 | work=Journal of the ACM | volume=13 | issue=4 | doi=10.1145/321356.321365}}
3. ^John E. Hopcroft and Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley Publishing, Reading Massachusetts, 1979. {{ISBN|0-201-02988-X}}., Ex. 11.1, pp. 282f

1 : Formal languages

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。