“Modular lambda function”的意思、由来-开放百科全书

In mathematics, the elliptic modular lambda function λ(τ) is a highly symmetric holomorphic function on the complex upper half-plane. It is invariant under the fractional linear action of the congruence group Γ(2), and generates the function field of the corresponding quotient, i.e., it is a Hauptmodul for the modular curve X(2). Over any point τ, its value can be described as a cross ratio of the branch points of a ramified double cover of the projective line by the elliptic curve

, where the map is defined as the quotient by the [−1] involution.

By symmetrizing the lambda function under the canonical action of the symmetric group S₃ on X(2), and then normalizing suitably, one obtains a function on the upper half-plane that is invariant under the full modular group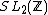

, and it is in fact Klein's modular j-invariant.

Modular properties

Consequently, the action of the modular group on

is that of the anharmonic group, giving the six values of the cross-ratio:^[3]

Other appearances

Other elliptic functions

It is the square of the Jacobi modulus,^[4] that is,

. In terms of the Dedekind eta function

and theta functions,^[4]

In terms of the half-periods of Weierstrass's elliptic functions, let

be a fundamental pair of periods with

Since the three half-period values are distinct, this shows that λ does not take the value 0 or 1.^[4]

Little Picard theorem

The lambda function is used in the original proof of the Little Picard theorem, that an entire non-constant function on the complex plane cannot omit more than one value. This theorem was proved by Picard in 1879.^[8] Suppose if possible that f is entire and does not take the values 0 and 1. Since λ is holomorphic, it has a local holomorphic inverse ω defined away from 0,1,∞. Consider the function z → ω(f(z)). By the Monodromy theorem this is holomorphic and maps the complex plane C to the upper half plane. From this it is easy to construct a holomorphic function from C to the unit disc, which by Liouville's theorem must be constant.^[9]

Moonshine

The function

is the normalized Hauptmodul for the group

, and its q-expansion

, {{oeis|id=A007248}} where

, is the graded character of any element in conjugacy class 4C of the monster group acting on the monster vertex algebra.

Footnotes

1. ^Chandrasekharan (1985) p.115
2. ^Chandrasekharan (1985) p.109
3. ^Chandrasekharan (1985) p.110
4. ^¹²³Chandrasekharan (1985) p.108
5. ^Chandrasekharan (1985) p.63
6. ^Chandrasekharan (1985) p.117
7. ^Rankin (1977) pp.226–228
8. ^Chandrasekharan (1985) p.121
9. ^Chandrasekharan (1985) p.118

References

{{Citation | editor1-last=Abramowitz | editor1-first=Milton | editor1-link=Milton Abramowitz | editor2-last=Stegun | editor2-first=Irene A. | editor2-link=Irene Stegun | title=Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables | publisher=Dover Publications | location=New York | isbn=978-0-486-61272-0 | year=1972 | zbl=0543.33001 }}

{{citation | last=Chandrasekharan | first=K. | authorlink=K. S. Chandrasekharan | title=Elliptic Functions | series=Grundlehren der mathematischen Wissenschaften | volume=281 | publisher=Springer-Verlag | year=1985 | isbn=3-540-15295-4 | zbl=0575.33001 | pages=108–121 }}

{{citation|first1=John Horton|last1=Conway|author1-link=John Horton Conway|first2=Simon|last2=Norton|author2-link=Simon P. Norton|title=Monstrous moonshine|journal=Bulletin of the London Mathematical Society|volume=11|issue=3|year=1979|pages=308–339|mr=0554399|zbl=0424.20010 |doi=10.1112/blms/11.3.308}}

{{citation | last=Rankin | first=Robert A. | authorlink=Robert Alexander Rankin | title=Modular Forms and Functions | publisher=Cambridge University Press | year=1977 | isbn=0-521-21212-X | zbl=0376.10020 }}

{{dlmf|id=23.15.E6|title=Elliptic Modular Function|first= W. P. |last=Reinhardt|first2=P. L.|last2= Walker}}

2 : Modular forms|Elliptic functions