“Morphological gradient”的意思、由来-开放百科全书

词条

Morphological gradient

释义

Mathematical definition and types
References
External links

In mathematical morphology and digital image processing, a morphological gradient is the difference between the dilation and the erosion of a given image. It is an image where each pixel value (typically non-negative) indicates the contrast intensity in the close neighborhood of that pixel. It is useful for edge detection and segmentation applications.

Mathematical definition and types

Let 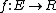be a grayscale image, mapping points from a Euclidean space or discrete grid E (such as R² or Z²) into the real line. Let be a grayscale structuring element. Usually, b is symmetric and has short-support, e.g.,

.

Then, the morphological gradient of f is given by:

,

where and denote the dilation and the erosion, respectively.

An internal gradient is given by:

,

and an external gradient is given by:

.

The internal and external gradients are "thinner" than the gradient, but the gradient peaks are located on the edges, whereas the internal and external ones are located at each side of the edges. Notice that .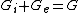

If 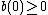, then all the three gradients have non-negative values at all pixels.

References

Image Analysis and Mathematical Morphology by Jean Serra, {{ISBN|0-12-637240-3}} (1982)
Image Analysis and Mathematical Morphology, Volume 2: Theoretical Advances by Jean Serra, {{ISBN|0-12-637241-1}} (1988)
An Introduction to Morphological Image Processing by Edward R. Dougherty, {{ISBN|0-8194-0845-X}} (1992)

External links

Morphological gradients, Centre de Morphologie Mathématique, École_des_Mines_de_Paris

2 : Mathematical morphology|Digital geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。