“Mountain climbing problem”的意思、由来-开放百科全书

词条

Mountain climbing problem

释义

Understanding the problem
Formulation
Proof in the piecewise linear case
Notes
References
External links

In mathematics, the mountain climbing problem is a problem of finding the conditions that two functions forming profiles of a two-dimensional mountain must satisfy, so that two climbers can start on the bottom on the opposite sides of the mountain and coordinate their movements to meet (possibly at the top) while always staying at the same height. This problem was named and posed in this form by {{harvs|first=James V.|last=Whittaker|year=1966|txt}}, but its history goes back to {{harvs|first=Tatsuo|last=Homma|year=1952|txt}}, who solved a version of it. The problem has been repeatedly rediscovered and solved independently in different context by a number of people (see the references).

In the past two decades the problem was shown to be connected to the weak Fréchet distance of curves in the plane,{{sfnp|Buchin|Buchin|Knauer|Rote|2007}} various planar motion planning problems in computational geometry,{{sfnp|Goodman|Pach|Yap|1989}} the inscribed square problem,{{sfnp|Pak|2010}} semigroup of polynomials,{{sfnp|Baird|Magill|1997}} etc. The problem was popularized in the article by {{harvtxt|Goodman|Pach|Yap|1989}}, which received the Mathematical Association of America's Lester R. Ford Award in 1990.^[1]

Understanding the problem

It is easy to coordinate the climbers' movement between the peaks and valleys (local maxima and minima of the functions). The difficulty is that to progress, the climbers must occasionally go down the mountain, either one or the other, or both climbers. Similarly, either one or the other climber must backtrack towards the beginning of the journey. In fact, it has been observed that for a mountain with {{mvar|n}} peaks and valleys the number of turns can be as large as quadratic in {{mvar|n}}.{{sfnp|Buchin|Buchin|Knauer|Rote|2007}} These complications make the problem unintuitive and sometimes rather difficult, both in theory and in practice.

Formulation

The following result is due to {{harvtxt|Huneke|1969}}:

Suppose and are continuous functions from to with and , and such that neither function is constant on an interval. Then there exist continuous functions and from to with , , and such that , where "" stands for a composition of functions.

On the other hand, it is not possible to extend this result to all continuous functions. For, if has constant height over an interval while has infinitely many oscillations that pass through the same height, then the first climber may be forced to go back and forth infinitely many times, and thus can never reach the top.

For the piecewise linear functions there are no obstructions. In this case, the climbers can always coordinate their movements to get to the top, regardless of whether there are intervals of constant height.{{sfnp|Whittaker|1966}}

Proof in the piecewise linear case

Suppose that both functions are piecewise linear, and do not have any intervals of constant height.

Consider the set of all pairs for which a first climber at and a second climber at would have the same height as each other.

If we interpret these pairs as the Cartesian coordinates of points in the plane, then this set is a union of line segments. It can be interpreted as the drawing of an undirected graph that has a vertex at each line segment endpoint or crossing, and an edge for each portion of a line segment that connects two vertices.

This graph may or may not be connected. It has vertices of the following types:

At the vertex 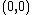the degree of the vertex (the number of incident edges) is one: the only possible direction for both climbers to go is onto the mountain. Similarly, at the degree is one, because both climbers can only return down the mountain.
At a vertex where neither climber is at a peak or a valley, then the degree is two: it is only possible for both climbers to go up, or both to go down.
At a vertex where one climber is at a peak or a valley and the other one is not, then the degree is again two: the climber at the peak or valley has two choices of which way to go, and the other climber can only go one way.
At a vertex where both climbers are at peaks or both climbers are at valleys, the degree is four: both climbers may choose independently of each other which direction to go.
The set of pairs used to define the graph may also include points where one climber is at a peak and the other is at a valley. These points may be interpreted as isolated vertices of : neither climber can move, so the degree is zero.

According to the handshaking lemma, every connected component of an undirected graph has an even number of odd-degree vertices.

Since the only odd-degree vertices are 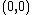and , these two vertices must belong to the same connected component. That is, there must be a path from 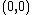to in . In the language of mountain climbers, this gives a way to coordinate the climbers' movement to reach the top of the mountain.

The proof for functions that are piecewise linear but that allow intervals of constant height is similar, but involves a more complicated case analysis. Alternatively, one can find a path for modified functions in which all the intervals of constant height have been collapsed to points, and then extend the resulting path to the original functions.

Notes

1. ^{{citation|url=http://www.maa.org/programs/maa-awards/writing-awards/mountain-climbing-ladder-moving-and-the-ring-width-of-a-polygon|title=Mountain Climbing, Ladder Moving, and the Ring-Width of a Polygon|work=Writing Awards|publisher=Mathematical Association of America|year=1990|accessdate=2015-12-19}}.

References

{{citation

and

relations for generalized polynomials
| volume = 55
| year = 1997}}.

{{citation

| last1 = Buchin | first1 = Kevin
| last2 = Buchin | first2 = Maike
| last3 = Knauer | first3 = Christian
| last4 = Rote | first4 = Günter
| last5 = Wenk | first5 = Carola
| contribution = How difficult is it to walk the dog?
| contribution-url = http://page.mi.fu-berlin.de/rote/Papers/abstract/How+difficult+is+it+to+walk+the+dog.html
| pages = 170–173
| title = Proc. 23rd European Workshop on Computational Geometry (Graz, 2007)
| year = 2007}}.

{{citation

| last1 = Goodman | first1 = Jacob E. | author1-link = Jacob E. Goodman
| last2 = Pach | first2 = János | author2-link = János Pach
| last3 = Yap | first3 = Chee-K.
| doi = 10.2307/2323971
| issue = 6
| journal = American Mathematical Monthly
| mr = 999412
| pages = 494–510
| title = Mountain climbing, ladder moving, and the ring-width of a polygon
| url = http://www.maa.org/sites/default/files/pdf/upload_library/22/Ford/Goodman-Pach-Yap494-510.pdf
| volume = 96
| year = 1989}}.

{{citation

| last = Homma | first = Tatsuo
| journal = Kōdai Mathematical Seminar Reports
| mr = 0049988
| pages = 13–16
| title = A theorem on continuous functions
| volume = 4
| year = 1952
| doi=10.2996/kmj/1138843207}}.

{{citation

| last = Huneke | first = John Philip
| journal = Transactions of the American Mathematical Society
| mr = 0239013
| pages = 383–391
| title = Mountain climbing
| volume = 139
| year = 1969
| doi=10.2307/1995331}}.

{{citation

| last = Jiménez López | first = Víctor
| doi = 10.1007/s000100050069
| issue = 1
| journal = Aequationes Mathematicae
| mr = 1675749
| pages = 45–49
| title = An elementary solution to the mountain climbers' problem
| volume = 57
| year = 1999}}.

{{citation

| last = Keleti | first = Tamás
| doi = 10.2307/2159702
| issue = 1
| journal = Proceedings of the American Mathematical Society
| mr = 1123655
| pages = 89–97
| title = The mountain climbers' problem
| volume = 117
| year = 1993}}.

{{citation

| last = Lipiński | first = J. S.
| journal = Bull. Acad. Polon. Sci. Cl. III
| mr = 0095224
| pages = 1019–1021, LXXXV
| title = Sur l'uniformisation des fonctions continues
| volume = 5
| year = 1957}}.

{{citation

| last = McKiernan | first = M. A.
| doi = 10.1007/BF02189402
| issue = 1-2
| journal = Aequationes Mathematicae
| mr = 781218
| pages = 132–134
| title = Mountain climbing: an alternate proof
| volume = 28
| year = 1985}}.

{{citation

| last = Mioduszewski | first = J.
| journal = Colloquium Mathematicum
| mr = 0143181
| pages = 233–240
| title = On a quasi-ordering in the class of continuous mappings of a closed interval into itself
| volume = 9
| year = 1962}}.

{{citation

| last = Pak | first = Igor | author-link = Igor Pak
| page = 39
| title = Lectures on Discrete and Polyhedral Geometry
| url = http://www.math.ucla.edu/~pak/book.htm
| year = 2010}}.

{{citation

| last1 = Sikorski | first1 = R.
| last2 = Zarankiewicz | first2 = K. | author2-link = Kazimierz Zarankiewicz
| journal = Fundamenta Mathematicae
| mr = 0072465
| pages = 339–344
| title = On uniformization of functions. I
| volume = 41
| year = 1955}}.

{{citation

| last = Tucker | first = Alan | authorlink = Alan Tucker
| journal = Math Horizons
| url = http://www.maa.org/sites/default/files/pdf/upload_library/22/Evans/november_1995_22.pdf
| volume = 3
| issue = 2
| pages = 22–24
| title = The parallel climbers puzzle
| year = 1995}}.

{{citation

| last = Whittaker | first = James V.
| doi = 10.4153/CJM-1966-087-x
| journal = Canadian Journal of Mathematics
| mr = 0196013
| pages = 873–882
| title = A mountain-climbing problem
| volume = 18
| year = 1966}}..

External links

The Parallel Mountain Climbers Problem, a description and a Java applet solution.

4 : Articles containing proofs|Discrete geometry|Recreational mathematics|Mathematical problems

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。