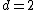1. Examples^[5][6]
    Positive powers  Negative powers  Fractional powers  Rendering along the exponent 

2. Rendering images
    Pseudocode   

3. References

In mathematics, a multibrot set is the set of values in the complex plane whose absolute value remains below some finite value throughout iterations by a member of the general monic univariate polynomial family of recursions.^[1][2][3] The name is a portmanteau of multiple and Mandelbrot set. The same can be applied to the Julia set, this being called Multi-Julia set.

where d ≥ 2. The exponent d may be further generalized to negative and fractional values.^[4]

Several graphics are available but, as far as can be verified, none of these have been taken a step further to display a 3-D stack of the various stages so that the evolution of the general shape can be seen from other than vertically above.

Examples^[5][6]

The case of

is the classic Mandelbrot set from which the name is derived.

The sets for other values of d also show fractal images^[7] when they are plotted on the complex plane.

Each of the examples of various powers d shown below is plotted to the same scale. Values of c belonging to the set are black. Values of c that have unbounded value under recursion, and thus do not belong in the set, are plotted in different colours, that show as contours, depending on the number of recursions that caused a value to exceed a fixed magnitude in the Escape Time algorithm.

Positive powers

The example {{nowrap|d {{=}} 2}} is the original Mandelbrot set. The examples for {{nowrap|d > 2}} are often called multibrot sets. These sets include the origin and have fractal perimeters, with {{nowrap|(d − 1)-fold}} rotational symmetry.

Negative powers

When d is negative the set surrounds but does not include the origin. There is interesting complex behaviour in the contours between the set and the origin, in a star-shaped area with {{nowrap|(1 − d)-fold}} rotational symmetry. The sets appear to have a circular perimeter, however this is just an artifact of the fixed maximum radius allowed by the Escape Time algorithm, and is not a limit of the sets that actually extend in all directions to infinity.

Fractional powers

Rendering along the exponent

An alternative method is to render the exponent along the vertical axis. This requires either fixing the real or the imaginary value, and rendering the remaining value along the horizontal axis. The resulting set rises vertically from the origin in a narrow column to infinity. Magnification reveals increasing complexity. The first prominent bump or spike is seen at an exponent of 2, the location of the traditional Mandelbrot set at its cross-section. The third image here renders on a plane that is fixed at a 45-degree angle between the real and imaginary axes.

Rendering images

All the above images are rendered using an Escape Time algorithm that identifies points outside the set in a simple way. Much greater fractal detail is revealed by plotting the Lyapunov exponent,^[9] as shown by the example below. The Lyapunov exponent is the error growth-rate of a given sequence. First calculate the iteration sequence with N iterations, then calculate the exponent as

and if the exponent is negative the sequence is stable. The white pixels in the picture are the parameters c for which the exponent is positive aka unstable. The colours show the periods of the cycles which the orbits are attracted to. All points colored dark-blue (outside) are attracted by a fixed point, all points in the middle (lighter blue) are attracted by a period 2 cycle and so on.

Pseudocode

ESCAPE TIME ALGORITHM

    For each pixel on the screen do:    {      x = x0 = x co-ordinate of pixel      y = y0 = y co-ordinate of pixel          iteration = 0      max_iteration = 1000          while ( x*x + y*y <= (2*2) AND iteration < max_iteration )      {        /* INSERT CODE(S)FOR Z^d FROM TABLE BELOW */            iteration = iteration + 1      }          if ( iteration == max_iteration )      then        colour = black      else        colour = iteration          plot(x0,y0,colour)    }

The complex value z has coordinates (x,y) on the complex plane and is raised to various powers inside the iteration loop by codes shown in this table. Powers not shown in the table can be obtained by concatenating the codes shown.

d=x^4+2*x^2*y^2+y^4if d=0 then ESCAPExtmp = (x^2-y^2)/d+ay = -2*x*y/d+bx = xtmp 

d=x^2+y^2if d=0 then ESCAPEx = x/d + ay= -y/d + b 

xtmp=x^2-y^2 + ay=2*x*y + bx=xtmp 

xtmp=x^3-3*x*y^2 + ay=3*x^2*y-y^3 + bx=xtmp 

xtmp=x^5-10*x^3*y^2+5*x*y^4 + ay=5*x^4*y-10*x^2*y^3+y^5 + bx=xtmp

xtmp=(x*x+y*y)^(n/2)*cos(n*atan2(y,x)) + ay=(x*x+y*y)^(n/2)*sin(n*atan2(y,x)) + bx=xtmp

References

• BlueStacks
• BlueStacks App Player
• Bluestack Way
• Blue Stahli discography
• Blue Star Contemporary Art Center
• Blue Starfish
• Blue Star Ithaki
• Blue Star Kachina
• Blue Star Line (2012- )
• Blue Star Line Cruises
• Bluestars
• Blue Stars (basketball club)
• Bluestars (Pretty Ricky album)
• Blue Startups
• Blue Star Turnpikes
• Blue star water lily
• Blue state (disambiguation)
• Blue State (disambiguation)
• Blue States (disambiguation)
• Bluestein's FFT algorithm
• Bluestem Lake
• Blue-stemmed goldenrod
• Blue-stemmed Goldenrod
• Blue-stemmed golden-rod
• Bluestem pricklypoppy