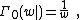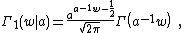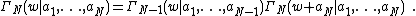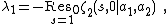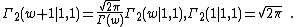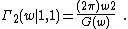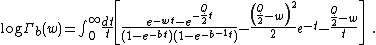- Definition
- Properties
- Infinite product representation
- Reduction to the Barnes G-function
- The double gamma function and conformal field theory
- References
- Further reading
In mathematics, the multiple gamma function 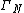 is a generalization of the Euler gamma function and the Barnes G-function. The double gamma function was studied by {{harvtxt|Barnes|1901}}. At the end of this paper he mentioned the existence of multiple gamma functions generalizing it, and studied these further in {{harvtxt|Barnes|1904}}.
is a generalization of the Euler gamma function and the Barnes G-function. The double gamma function was studied by {{harvtxt|Barnes|1901}}. At the end of this paper he mentioned the existence of multiple gamma functions generalizing it, and studied these further in {{harvtxt|Barnes|1904}}.
Double gamma functions  are closely related to the q-gamma function, and triple gamma functions
are closely related to the q-gamma function, and triple gamma functions 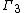 are related to the elliptic gamma function.
are related to the elliptic gamma function.
Definition
For  , let
, let
where 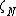 is the Barnes zeta function. (This differs by a constant from Barnes's original definition.)
is the Barnes zeta function. (This differs by a constant from Barnes's original definition.)
Properties
Considered as a meromorphic function of  ,
, 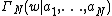 has no zeros. It has poles at
has no zeros. It has poles at 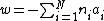 for non-negative integers
for non-negative integers  . These poles are simple unless some of them coincide. Up to multiplication by the exponential of a polynomial,
. These poles are simple unless some of them coincide. Up to multiplication by the exponential of a polynomial, 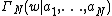 is the unique meromorphic function of finite order with these zeros and poles.
is the unique meromorphic function of finite order with these zeros and poles.
Infinite product representation
The multiple Gamma function has an infinite product representation that makes it manifest that it is meromorphic, and that also makes the positions of its poles manifest. In the case of the double Gamma function, this representation is [1]
where we define the  -independent coefficients
-independent coefficients
where 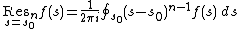 is an
is an  -th order residue at
-th order residue at  .
.
Reduction to the Barnes G-function
The double Gamma function with parameters  obeys the relations [1]
obeys the relations [1]
It is related to the Barnes G-function by
The double gamma function and conformal field theory
For  and
and 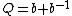 , the function
, the function
is invariant under  , and obeys the relations
, and obeys the relations
For  , it has the integral representation
, it has the integral representation
From the function  , we define the double Sine function
, we define the double Sine function  and the Upsilon function
and the Upsilon function 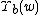 by
by
These functions obey the relations
plus the relations that are obtained by  . For
. For  they have the integral representations
they have the integral representations
The functions  and
and  appear in correlation functions of two-dimensional conformal field theory, with the parameter
appear in correlation functions of two-dimensional conformal field theory, with the parameter  being related to the central charge of the underlying Virasoro algebra.[2] In particular, the three-point function of Liouville theory is written in terms of the function
being related to the central charge of the underlying Virasoro algebra.[2] In particular, the three-point function of Liouville theory is written in terms of the function  .
.
References
2. ^{{Citation | last1=Ponsot | first1=B. |title=Recent progress on Liouville Field Theory | arxiv=hep-th/0301193|publisher = arXiv:hep-th/0301193|bibcode=2003PhDT.......180P}}
Further reading
- {{citation|first=E. W. |last=Barnes
|title= The Genesis of the Double Gamma Functions
|journal= Proc. London Math. Soc. |year=1899 |volume=s1-31|pages= 358–381| doi=10.1112/plms/s1-31.1.358 }}
- {{Citation | last1=Barnes | first1=E. W. | title=The Theory of the Double Gamma Function. [Abstract] | jstor=116064 | publisher=The Royal Society | year=1899 | journal=Proceedings of the Royal Society of London | issn=0370-1662 | volume=66 | pages=265–268 | doi=10.1098/rspl.1899.0101}}
- {{Citation | last1=Barnes | first1=E. W. | title=The Theory of the Double Gamma Function | jstor=90809 | publisher=The Royal Society | year=1901 | journal=Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character | issn=0264-3952 | volume=196 | pages=265–387 | doi=10.1098/rsta.1901.0006| bibcode=1901RSPTA.196..265B }}
- {{citation|first=E. W. |last=Barnes|title=On the theory of the multiple gamma function|journal= Trans. Camb. Philos. Soc. |volume=19 |year=1904|pages=374–425}}
- {{Citation | last1=Friedman | first1=Eduardo | last2=Ruijsenaars | first2=Simon | title=Shintani–Barnes zeta and gamma functions | doi=10.1016/j.aim.2003.07.020 | mr=2078341 | year=2004 | journal=Advances in Mathematics | issn=0001-8708 | volume=187 | issue=2 | pages=362–395}}
- {{Citation | last1=Ruijsenaars | first1=S. N. M. | title=On Barnes' multiple zeta and gamma functions | doi=10.1006/aima.2000.1946 | mr=1800255 | year=2000 | journal=Advances in Mathematics | issn=0001-8708 | volume=156 | issue=1 | pages=107–132}}
- Poussey
- Poussey Washington
- Poustis
- Poustka (Cheb District)
- Poutasi (disambiguation)
- Pouta (song)
- Poutavanh Phengthalangsy
- Pouteria contermina
- Pouteria danikeri
- Pouteria kaalaensis
- Pouteria pinifolia
- Pouteria torta
- Pouthak
- Poutineries
- Poutou
- Poutrincourt Lake
- Poutsma
- Poutsma, Stefan
- Poutza
- Poutūterangi
- Pouvalu Latukefu
- Pou Vannary
- Pouvoir Intime
- Pouya Idani
- Pouya Saraei