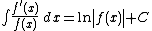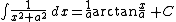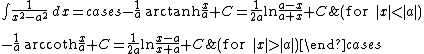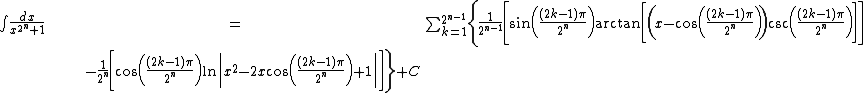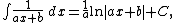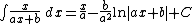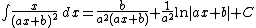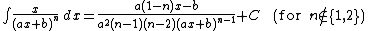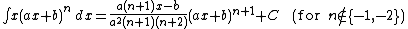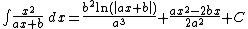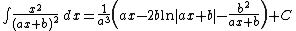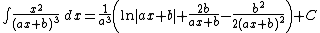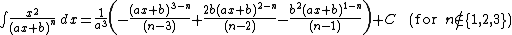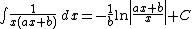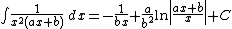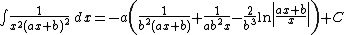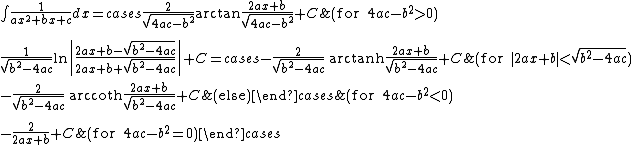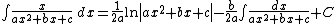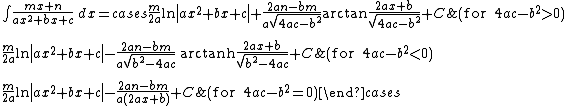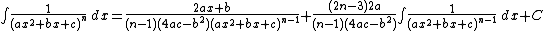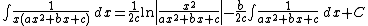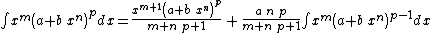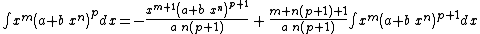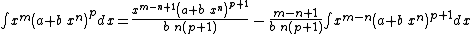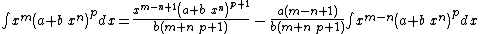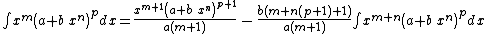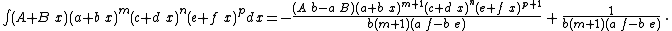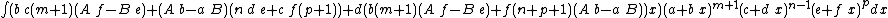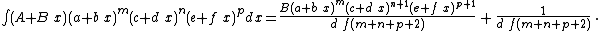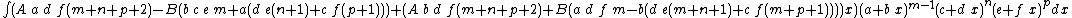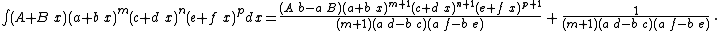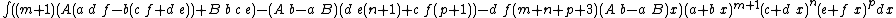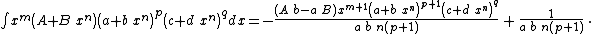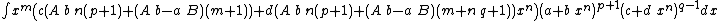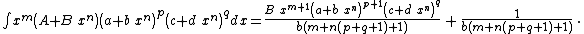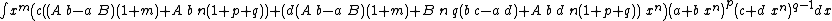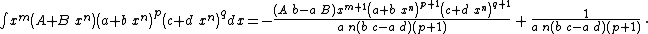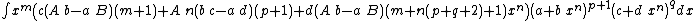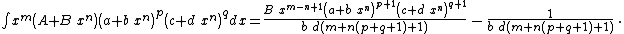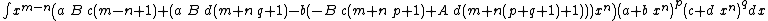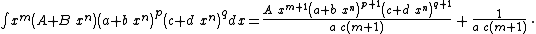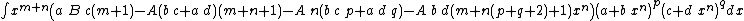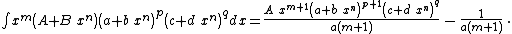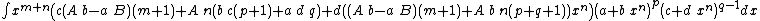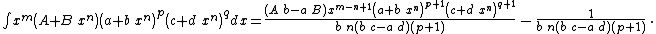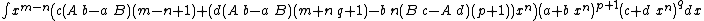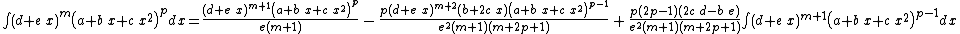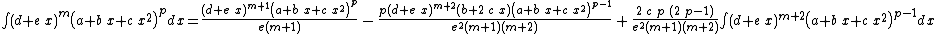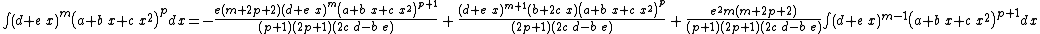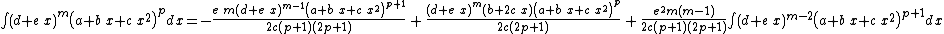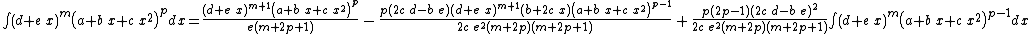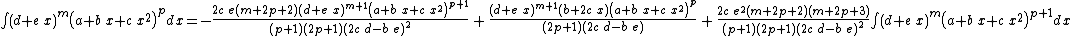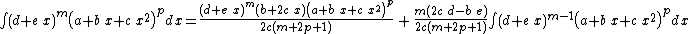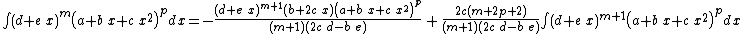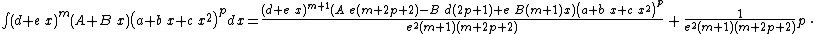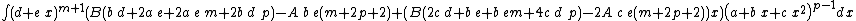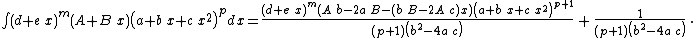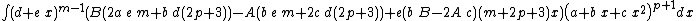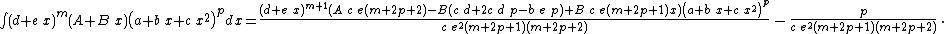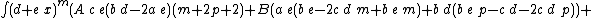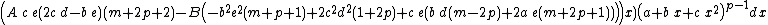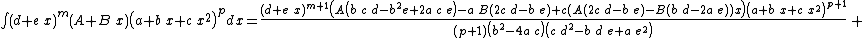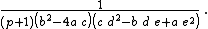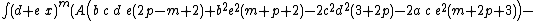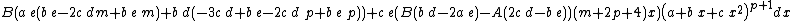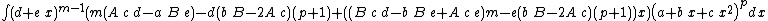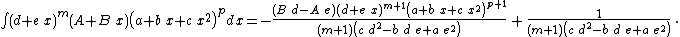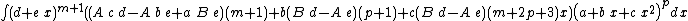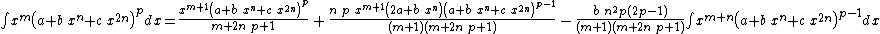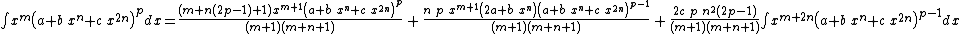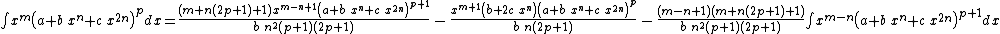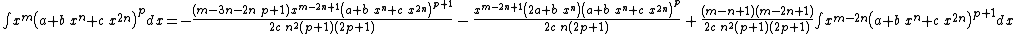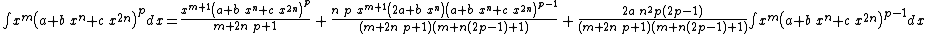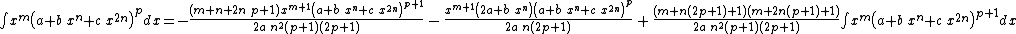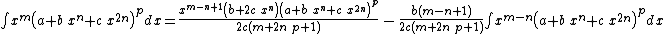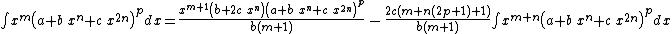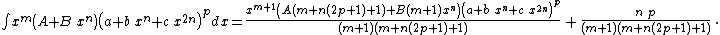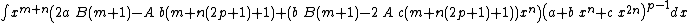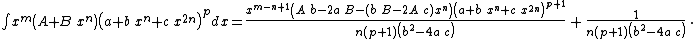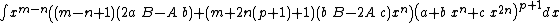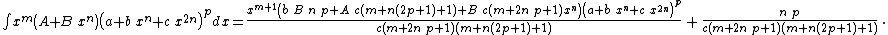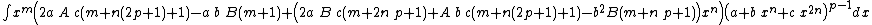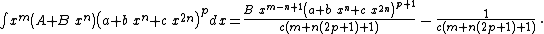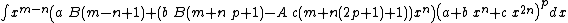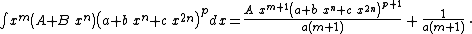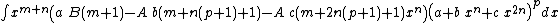“List of integrals of rational functions”的意思、由来-开放百科全书

　

词条

List of integrals of rational functions

释义

Miscellaneous integrands
Integrands of the form x^m(a x + b)ⁿ
Integrands of the form x^m / (a x² + b x + c)ⁿ
Integrands of the form x^m (a + b xⁿ)^p
Integrands of the form (A + B x) (a + b x)^m (c + d x)ⁿ (e + f x)^p
Integrands of the form x^m (A + B xⁿ) (a + b xⁿ)^p (c + d xⁿ)^q
Integrands of the form (d + e x)^m (a + b x + c x²)^p when b² − 4 a c = 0
Integrands of the form (d + e x)^m (A + B x) (a + b x + c x²)^p
Integrands of the form x^m (a + b xⁿ + c x²ⁿ)^p when b² − 4 a c = 0
Integrands of the form x^m (A + B xⁿ) (a + b xⁿ + c x²ⁿ)^p
References

The following is a list of integrals (antiderivative functions) of rational functions.

Any rational function can be integrated by partial fraction decomposition of the function into a sum of functions of the form:

, and

which can then be integrated term by term.

For other types of functions, see lists of integrals.

Miscellaneous integrands

Integrands of the form x^m(a x + b)ⁿ

Many of the following antiderivatives have a term of the form ln |ax + b|. Because this is undefined when x = −b / a, the most general form of the antiderivative replaces the constant of integration with a locally constant function.^[1] However, it is conventional to omit this from the notation. For example,

is usually abbreviated as

where C is to be understood as notation for a locally constant function of x. This convention will be adhered to in the following.

(Cavalieri's quadrature formula)

Integrands of the form x^m / (a x² + b x + c)ⁿ

For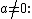

Integrands of the form x^m (a + b xⁿ)^p

The resulting integrands are of the same form as the original integrand, so these reduction formulas can be repeatedly applied to drive the exponents m and p toward 0.
These reduction formulas can be used for integrands having integer and/or fractional exponents.

Integrands of the form (A + B x) (a + b x)^m (c + d x)ⁿ (e + f x)^p

The resulting integrands are of the same form as the original integrand, so these reduction formulas can be repeatedly applied to drive the exponents m, n and p toward 0.
These reduction formulas can be used for integrands having integer and/or fractional exponents.
Special cases of these reductions formulas can be used for integrands of the form 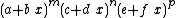by setting B to 0.

Integrands of the form x^m (A + B xⁿ) (a + b xⁿ)^p (c + d xⁿ)^q

The resulting integrands are of the same form as the original integrand, so these reduction formulas can be repeatedly applied to drive the exponents m, p and q toward 0.
These reduction formulas can be used for integrands having integer and/or fractional exponents.
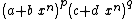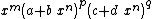Special cases of these reductions formulas can be used for integrands of the form and by setting m and/or B to 0.

Integrands of the form (d + e x)^m (a + b x + c x²)^p when b² − 4 a c = 0

The resulting integrands are of the same form as the original integrand, so these reduction formulas can be repeatedly applied to drive the exponents m and p toward 0.
These reduction formulas can be used for integrands having integer and/or fractional exponents.
Special cases of these reductions formulas can be used for integrands of the form when 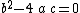by setting m to 0.

Integrands of the form (d + e x)^m (A + B x) (a + b x + c x²)^p

The resulting integrands are of the same form as the original integrand, so these reduction formulas can be repeatedly applied to drive the exponents m and p toward 0.
These reduction formulas can be used for integrands having integer and/or fractional exponents.
Special cases of these reductions formulas can be used for integrands of the form and by setting m and/or B to 0.

Integrands of the form x^m (a + b xⁿ + c x²ⁿ)^p when b² − 4 a c = 0

The resulting integrands are of the same form as the original integrand, so these reduction formulas can be repeatedly applied to drive the exponents m and p toward 0.
These reduction formulas can be used for integrands having integer and/or fractional exponents.
Special cases of these reductions formulas can be used for integrands of the form 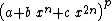when 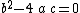by setting m to 0.

Integrands of the form x^m (A + B xⁿ) (a + b xⁿ + c x²ⁿ)^p

The resulting integrands are of the same form as the original integrand, so these reduction formulas can be repeatedly applied to drive the exponents m and p toward 0.
These reduction formulas can be used for integrands having integer and/or fractional exponents.
Special cases of these reductions formulas can be used for integrands of the form 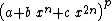and 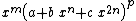by setting m and/or B to 0.

References

1. ^"Reader Survey: log|x| + C", Tom Leinster, The n-category Café, March 19, 2012

{{Lists of integrals}}

2 : Integrals|Mathematics-related lists

随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号更新时间：2024/11/17 15:20:34