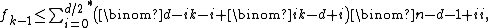1. References

In geometry and polyhedral combinatorics, a k-neighborly polytope is a convex polytope in which every set of k or fewer vertices forms a face. For instance, a 2-neighborly polytope is a polytope in which every pair of vertices is connected by an edge, forming a complete graph. 2-neighborly polytopes with more than four vertices may exist only in spaces of four or more dimensions, and in general a k-neighborly polytope (other than a simplex) requires a dimension of 2k or more. A d-simplex is d-neighborly. A polytope is said to be neighborly, without specifying k, if it is k-neighborly for 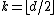. If we exclude simplices, this is the maximum possible k: in fact, every polytope that is k-neighborly for some 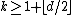is a simplex.^[1]

In a k-neighborly polytope with k ≥ 3, every 2-face must be a triangle, and in a k-neighborly polytope with k ≥ 4, every 3-face must be a tetrahedron. More generally, in any k-neighborly polytope, all faces of dimension less than k are simplices.

The cyclic polytopes formed as the convex hulls of finite sets of points on the moment curve (t, t², ..., t^d) in d-dimensional space are automatically neighborly. Theodore Motzkin conjectured that all neighborly polytopes are combinatorially equivalent to cyclic polytopes.^[2] However, contrary to this conjecture, there are many neighborly polytopes that are not cyclic: the number of combinatorially distinct neighborly polytopes grows superexponentially, both in the number of vertices of the polytope and in the dimension.^[3]

The convex hull of a set of random points, drawn from a Gaussian distribution with the number of points proportional to the dimension, is with high probability k-neighborly for a value k that is also proportional to the dimension.^[4]

The number of faces of all dimensions of a neighborly polytope in an even number of dimensions is determined solely from its dimension and its number of vertices by the Dehn–Sommerville equations: the number of k-dimensional faces, f_k, satisfies the inequality

where the asterisk means that the sums ends at 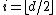and final term of the sum should be halved if d is even.^[5] According to the upper bound theorem of {{harvtxt|McMullen|1970}},^[6] neighborly polytopes achieve the maximum possible number of faces of any n-vertex d-dimensional convex polytope.

A generalized version of the happy ending problem applies to higher-dimensional point sets, and imples that

for every dimension d and every n > d there exists a number m(d,n) with the property that every m points in general position in d-dimensional space contain a subset of n points that form the vertices of a neighborly polytope.^[7]

References

• Sudebnik of Kazimir
• Sudecka Philharmonic
• Sudecka Philharmonic Orchestra
• Sudeck's atrophy
• Sudeck's syndrome
• Sudeep Chatterjee
• Sudeep Chatterjee (cinematographer)
• Sudeep Tyagi
• Sudeikis
• Sudejov
• Sudell (ward)
• Sudemäe
• Sudende railway station
• Sudene
• Sudentaival
• Sudeoksan
• Sudeok Station
• S. U. Deraniyagala
• S.U. Deraniyagala
• S U Deraniyagala
• SU Deraniyagala
• Suderau
• Suderbrarup
• Suderbrarup (Amt)
• Suderdeich