- Rational numbers Natural numbers Powers of ten (scientific notation) Integers Notable integers Named numbers Prime numbers Highly composite numbers Perfect numbers Cardinal numbers Small numbers English names for powers of 10 {{anchor|Myriad system}} Myriad, Octad, and -yllion systems SI prefixes for powers of 10 {{anchor|Fractional numbers}} Fractional numbers
- Irrational and suspected irrational numbers Algebraic numbers Transcendental numbers Suspected transcendentals Numbers not known with high precision
- Hypercomplex numbers Algebraic complex numbers Other hypercomplex numbers
- Transfinite numbers
- Numbers representing measured quantities
- Numbers representing physical quantities
- Numbers without specific values
- See also
- Notes
- Further reading
- External links
This is a list of articles about numbers (not about numerals).
This article is infinitely incomplete.
Rational numbers
{{main|Rational number}}A rational number is any number that can be expressed as the quotient or fraction {{math|p/q}} of two integers, a numerator {{math|p}} and a non-zero denominator {{math|q}}.[1] Since {{math|q}} may be equal to 1, every integer is a rational number. The set of all rational numbers, often referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by a boldface {{math|Q}} (or blackboard bold  , Unicode ℚ);[2] it was thus denoted in 1895 by Giuseppe Peano after quoziente, Italian for "quotient".
, Unicode ℚ);[2] it was thus denoted in 1895 by Giuseppe Peano after quoziente, Italian for "quotient".
Natural numbers
{{main|Natural number}}Natural numbers are those used for counting (as in "there are six (6) coins on the table") and ordering (as in "this is the third (3rd) largest city in the country"). In common language, words used for counting are "cardinal numbers" and words used for ordering are "ordinal numbers". There are infinitely many natural numbers.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |
| 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 |
| 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 |
| 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 |
| 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 |
| 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 |
| 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 |
| 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 |
| 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 |
| 150 | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 |
| 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 |
| 170 | 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 |
| 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 |
| 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 |
| 200 | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 |
| 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 |
| 220 | 221 | 222 | 223 | 224 | 225 | 226 | 227 | 228 | 229 |
| 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 |
| 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 |
| 250 | 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 |
| 260 | 270 | 280 | 290 | ||||||
| 300 | 400 | 500 | 600 | 700 | 800 | 900 | |||
| 1000 | 2000 | 3000 | 4000 | 5000 | 6000 | 7000 | 8000 | 9000 | |
| 10000 | 20000 | 30000 | 40000 | 50000 | 60000 | 70000 | 80000 | 90000 | |
| 105 | 106 | 107 | 108 | 109 | |||||
| 1010 | 10100 | 1010100 | Larger numbers | ||||||
(Note that the status of 0 is ambiguous. In set theory and computer science, 0 is considered a natural number. In number theory, it usually is not.)
Powers of ten (scientific notation)
{{Main|Orders of magnitude (numbers)}}A power of ten is a number 10k, where k is an integer. For instance, with k = 0, 1, 2, 3, ..., the appropriate powers of ten are 1, 10, 100, 1000, ... Powers of ten can also be fractional: for instance, k = -3 gives 1/1000, or 0.001.
In scientific notation, real numbers are written in the form m × 10n. The number 394,000 is written in this form as 3.94 × 105.
Integers
{{main|Integer}}Notable integers
Integers that are notable for their mathematical properties or cultural meanings include:
- −40, the equal point in the Fahrenheit and Celsius scales.
- −1, the additive inverse of unity.
- 0, the additive identity.
- 1, the multiplicative identity. Also the only natural number (not including 0) that isn't prime or composite.
- 2, the base of the binary number system, used in almost all modern computers and information systems. Also notable as the only even prime number.
- 3, significant in Christianity as the Trinity. Also considered significant in Hinduism (Trimurti, Tridevi). Holds significance in a number of ancient mythologies.
- 4, the first composite number, also considered an "unlucky number" in modern China, Japan and Korea due to its audible similarity to the word "Death."
- 5, number of fingers or toes for almost all amphibians, reptiles and mammals
- 6, the first of the series of perfect numbers, whose proper factors sum to the number itself.
- 7, considered a "lucky" number in Western cultures.
- 8, considered a "lucky" number in Chinese culture. It is also the number of bits in a byte
- 9, the first odd number that is composite. Also a significant number in Norse Mythology.
- 10, the number base for most modern counting systems.
- 11, the fifth prime and first palindromic multi-digit number
- 12, the number base for some ancient counting systems and the basis for some modern measuring systems. Known as a dozen.
- 13, considered an "unlucky" number in Western superstition. Also known as a "Baker's Dozen".
- 14, the number of days in a fortnight.
- 15, the number of players on a rugby union team. It is also the first point received in tennis.
- 16, the base of the hexadecimal number system which is utilized within many programming languages.
- 17, the sum of the first 4 prime numbers, and the only prime which is the sum of 4 consecutive primes.
- 18, age of majority in most countries in the world.
- 19, the length of one side of a Go board.
- 20, known as a score.
- 21, the legal drinking age in the United States.
- 22, the namesake of catch-22, a paradoxical condition in which there is no escape due to mutually conflicting or dependent conditions.
- 23, number of chromosomes in a human haploid. Other human cells have 23 pairs of chromosomes.
- 25, the first centered square number besides 1 that is also a square number. It is also the number of cents in a quarter.
- 28, the second perfect number.
- 42, the "answer to the ultimate question of life, the universe, and everything" in the popular science fiction work The Hitchhiker's Guide to the Galaxy.
- 60, the number base for some ancient counting systems, such as the Babylonians', and the basis for many modern measuring systems.
- 69, used as slang to refer to a sexual act.
- 86, a slang term that is used in the American popular culture as a transitive verb to mean throw out or get rid of.[3]
- 108, considered sacred by the Dharmic Religions. Approximately equal to the ratio of the distance from Earth to Sun and diameter of the Sun.
- 144, a dozen times dozen, known as a gross.
- 255, 28 − 1, a Mersenne number and the smallest perfect totient number that is neither a power of three nor thrice a prime; it is also the largest number that can be represented using an 8-bit unsigned integer.
- 256, The number of possible combinations within 8 bits, or a byte.
- 420, a code-term that refers to the consumption of cannabis.
- 496, the third perfect number.
- 666, the Number of the Beast from the Book of Revelation.
- 786, regarded as sacred in the Muslim Abjad numerology.
- 1024, the number of bytes in a kibibyte. It's also the number of bits in a kibibit.
- 1729, the Hardy–Ramanujan number, also known as the second taxicab number; that is, the smallest positive integer that can be written as the sum of two positive cubes in two different ways.[4]
- 5040, mentioned by Plato in the Laws as one of the most important numbers for the city. It is also the largest factorial (7! = 5040) that is also a highly composite number.
- 8128, the fourth perfect number.
- 65535, 216 − 1, the maximum value of a 16-bit unsigned integer.
- 65536, 216, the number of possible 16-bit combinations.
- 65537, 216 + 1, the most popular RSA public key prime exponent in most SSL/TLS certificates on the Web/Internet.
- 142857, the smallest base 10 cyclic number.
- 2147483647, 231 − 1, the maximum value of a 32-bit signed integer using two's complement representation.
- 9814072356, the largest perfect power that contains no repeated digits in base ten.
- 9223372036854775807, 263 − 1, the maximum value of a 64-bit signed integer using two's complement representation.
Named numbers
- Googol (10100) and googolplex (10(10100)) and googolplexian (10(10(10100))) or 1 followed by a googolplex of zeros.
- Graham's number
- Moser's number
- Shannon number
- Hardy–Ramanujan number (1729)
- Skewes' number
- Avogadro's number
- Kaprekar's constant (6174)
Prime numbers
{{Main|Prime number}}A prime number is a positive integer which has exactly two divisors: 1 and itself.
The first 100 prime numbers are:
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 |
| 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 | 113 |
| 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 |
| 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 | 229 |
| 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 |
| 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 |
| 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 | 541 |
Highly composite numbers
{{main|Highly composite number}}A highly composite number (HCN) is a positive integer with more divisors than any smaller positive integer. They are often used in geometry, grouping and time measurement.
The first 20 highly composite numbers are:
1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040, 7560.
Perfect numbers
{{main|Perfect number}}A perfect number is an integer that is the sum of its positive proper divisors (all divisors except itself).
The first 10 perfect numbers:
| 1 | 6 |
|---|---|
| 2 | 28 |
| 3 | 496 |
| 4 | 8 128 |
| 5 | 33 550 336 |
| 6 | 8 589 869 056 |
| 7 | 137 438 691 328 |
| 8 | 2 305 843 008 139 952 128 |
| 9 | 2 658 455 991 569 831 744 654 692 615 953 842 176 |
| 10 | 191 561 942 608 236 107 294 793 378 084 303 638 130 997 321 548 169 216 |
Cardinal numbers
{{main|cardinal number}}In the following tables, [and] indicates that the word and is used in some dialects (such as British English), and omitted in other dialects (such as American English).
Small numbers
This table demonstrates the standard English construction of small cardinal numbers up to one hundred million—names for which all variants of English agree.
| Value | Name | Alternate names, and names for sets of the given size |
|---|---|---|
| 0 | Zero | aught, cipher, cypher, donut, dot, duck, goose egg, love, nada, naught, nil, none, nought, nowt, null, ought, oh, squat, zed, zilch, zip, zippo, Sunya (Sanskrit) |
| 1 | One | ace, individual, single, singleton, unary, unit, unity, Pratham(Sanskrit) |
| 2 | Two | binary, brace, couple, couplet, distich, deuce, double, doubleton, duad, duality, duet, duo, dyad, pair, span, twain, twin, twosome, yoke |
| 3 | Three | deuce-ace, leash, set, tercet, ternary, ternion, terzetto, threesome, tierce, trey, triad, trine, trinity, trio, triplet, troika, hat-trick |
| 4 | Four | foursome, quadruplet, quatern, quaternary, quaternity, quartet, tetrad |
| 5 | Five | cinque, fin, fivesome, pentad, quint, quintet, quintuplet |
| 6 | Six | half dozen, hexad, sestet, sextet, sextuplet, sise |
| 7 | Seven | heptad, septet, septuple, walking stick |
| 8 | Eight | octad, octave, octet, octonary, octuplet, ogdoad |
| 9 | Nine | ennead |
| 10 | Ten | deca, decade, das (India) |
| 11 | Eleven | onze, ounze, ounce, banker's dozen |
| 12 | Twelve | dozen |
| 13 | Thirteen | baker's dozen, long dozen[5] |
| 14 | Fourteen | |
| 15 | Fifteen | |
| 16 | Sixteen | |
| 17 | Seventeen | |
| 18 | Eighteen | |
| 19 | Nineteen | |
| 20 | Twenty | score, |
| 21 | Twenty-one | long score[5], blackjack |
| 22 | Twenty-two | Deuce-deuce |
| 23 | Twenty-three | |
| 24 | Twenty-four | two dozen |
| 25 | Twenty-five | |
| 26 | Twenty-six | |
| 27 | Twenty-seven | |
| 28 | Twenty-eight | |
| 29 | Twenty-nine | |
| 30 | Thirty | |
| 31 | Thirty-one | |
| 32 | Thirty-two | |
| 33 | Thirty-three | |
| 34 | Thirty-four | |
| 35 | Thirty-five | |
| 40 | Forty | two-score |
| 41 | Forty-one | |
| 42 | Forty-two | |
| 45 | Forty-five | |
| 50 | Fifty | half-century |
| 55 | Fifty-five | double nickel |
| 60 | Sixty | three-score |
| 70 | Seventy | three-score and ten |
| 80 | Eighty | four-score |
| 87 | Eighty-seven | four-score and seven |
| 90 | Ninety | four-score and ten |
| 100 | One hundred | centred, century, ton, short hundred |
| 101 | One hundred [and] one | |
| 110 | One hundred [and] ten | |
| 111 | One hundred [and] eleven | eleventy-one[6] |
| 120 | One hundred [and] twenty | long hundred,[5] great hundred, (obsolete) hundred |
| 121 | One hundred [and] twenty-one | |
| 144 | One hundred [and] forty-four | gross, dozen dozen, small gross |
| 200 | Two hundred | |
| 300 | Three hundred | |
| 400 | Four hundred | |
| 500 | Five hundred | |
| 600 | Six hundred | |
| 666 | Six hundred [and] sixty-six | |
| 700 | Seven hundred | |
| 777 | Seven hundred [and] seventy-seven | |
| 800 | Eight hundred | |
| 900 | Nine hundred | |
| {{gaps|1|000}} | One thousand | chiliad, grand, G, thou, yard, kilo, k, millennium, Hajaar (India) |
| {{gaps|1|001}} | One thousand [and] one | |
| {{gaps|1|010}} | One thousand [and] ten | |
| {{gaps|1|011}} | One thousand [and] eleven | |
| {{gaps|1|024}} | One thousand [and] twenty-four | kibi or kilo in computing, see binary prefix (kilo is shortened to K, Kibi to Ki) |
| {{gaps|1|100}} | One thousand one hundred | Eleven hundred |
| {{gaps|1|101}} | One thousand one hundred [and] one | |
| {{gaps|1|728}} | One thousand seven hundred [and] twenty-eight | great gross, long gross, dozen gross |
| {{gaps|2|000}} | Two thousand | |
| {{gaps|3|000}} | Three thousand | |
| {{gaps|10|000}} | Ten thousand | myriad, wan (China) |
| {{gaps|100|000}} | One hundred thousand | lakh |
| {{gaps|500|000}} | Five hundred thousand | crore (Iranian) |
| {{gaps|1|000|000}} | One million | Mega, meg, mil, (often shortened to M) |
| {{gaps|1|048|576}} | One million forty-eight thousand five hundred [and] seventy-six | Mibi or Mega in computing, see binary prefix (Mega is shortened to M, Mibi to Mi) |
| {{gaps|10|000|000}} | Ten million | crore (Indian)(Pakistan) |
| {{gaps|100|000|000}} | One hundred million | yi (China) |
English names for powers of 10
This table compares the English names of cardinal numbers according to various American, British, and Continental European conventions. See English numerals or names of large numbers for more information on naming numbers.
| Short scale | Long scale | Power | |||
|---|---|---|---|---|---|
| Value | American | British (Nicolas Chuquet) | Continental European (Jacques Peletier du Mans) | of a thousand | of a million |
| 100 | One | 1000−1+1 | 10000000 | ||
| 101 | Ten | ||||
| 102 | Hundred | ||||
| 103 | Thousand | 10000+1 | 10000000.5 | ||
| 106 | Million | 10001+1 | 10000001 | ||
| 109 | Billion | Thousand million | Milliard | 10002+1 | 10000001.5 |
| 1012 | Trillion | Billion | 10003+1 | 10000002 | |
| 1015 | Quadrillion | Thousand billion | Billiard | 10004+1 | 10000002.5 |
| 1018 | Quintillion | Trillion | 10005+1 | 10000003 | |
| 1021 | Sextillion | Thousand trillion | Trilliard | 10006+1 | 10000003.5 |
| 1024 | Septillion | Quadrillion | 10007+1 | 10000004 | |
| 1027 | Octillion | Thousand quadrillion | Quadrilliard | 10008+1 | 10000004.5 |
| 1030 | Nonillion | Quintillion | 10009+1 | 10000005 | |
| 1033 | Decillion | Thousand quintillion | Quintilliard | 100010+1 | 10000005.5 |
| 1036 | Undecillion | Sextillion | 100011+1 | 10000006 | |
| 1039 | Duodecillion | Thousand sextillion | Sextilliard | 100012+1 | 10000006.5 |
| 1042 | Tredecillion | Septillion | 100013+1 | 10000007 | |
| 1045 | Quattuordecillion | Thousand septillion | Septilliard | 100014+1 | 10000007.5 |
| 1048 | Quindecillion | Octillion | 100015+1 | 10000008 | |
| 1051 | Sexdecillion | Thousand octillion | Octilliard | 100016+1 | 10000008.5 |
| 1054 | Septendecillion | Nonillion | 100017+1 | 10000009 | |
| 1057 | Octodecillion | Thousand nonillion | Nonilliard | 100018+1 | 10000009.5 |
| 1060 | Novemdecillion | Decillion | 100019+1 | 100000010 | |
| 1063 | Vigintillion | Thousand decillion | Decilliard | 100020+1 | 100000010.5 |
| 1066 | Unvigintillion | Undecillion | 100021+1 | 100000011 | |
| 1069 | Duovigintillion | Thousand undecillion | Undecilliard | 100022+1 | 100000011.5 |
| 1072 | Trevigintillion | Duodecillion | 100023+1 | 100000012 | |
| 1075 | Quattuorvigintillion | Thousand duodecillion | Duodecilliard | 100024+1 | 100000012.5 |
| 1078 | Quinvigintillion | Tredecillion | 100025+1 | 100000013 | |
| 1081 | Sexvigintillion | Thousand tredecillion | Tredecilliard | 100026+1 | 100000013.5 |
| 1084 | Septenvigintillion | Quattuordecillion | 100027+1 | 100000014 | |
| 1087 | Octovigintillion | Thousand quattuordecillion | Quattuordecilliard | 100028+1 | 100000014.5 |
| 1090 | Novemvigintillion | Quindecillion | 100029+1 | 100000015 | |
| 1093 | Trigintillion | Thousand quindecillion | Quindecilliard | 100030+1 | 100000015.5 |
| 1096 | Untrigintillion | Sexdecillion | 100031+1 | 100000016 | |
| 1099 | Duotrigintillion | Thousand sexdecillion | Sexdecilliard | 100032+1 | 100000016.5 |
| ... | ... | ... | ... | ... | |
| 10120 | Novemtrigintillion | Vigintillion | 100039+1 | 100000020 | |
| 10123 | Quadragintillion | Thousand vigintillion | Vigintilliard | 100040+1 | 100000020.5 |
| ... | ... | ... | ... | ... | |
| 10153 | Quinquagintillion | Thousand quinvigintillion | Quinvigintilliard | 100050+1 | 100000025.5 |
| ... | ... | ... | ... | ... | |
| 10180 | Novemquinquagintillion | Trigintillion | 100059+1 | 100000030 | |
| 10183 | Sexagintillion | Thousand trigintillion | Trigintilliard | 100060+1 | 100000030.5 |
| ... | ... | ... | ... | ... | |
| 10213 | Septuagintillion | Thousand quintrigintillion | Quintrigintilliard | 100070+1 | 100000035.5 |
| ... | ... | ... | ... | ... | |
| 10240 | Novemseptuagintillion | Quadragintillion | 100079+1 | 100000040 | |
| 10243 | Octogintillion | Thousand quadragintillion | Quadragintilliard | 100080+1 | 100000040.5 |
| ... | ... | ... | ... | ... | |
| 10273 | Nonagintillion | Thousand quinquadragintillion | Quinquadragintilliard | 100090+1 | 100000045.5 |
| ... | ... | ... | ... | ... | |
| 10300 | Novemnonagintillion | Quinquagintillion | 100099+1 | 100000050 | |
| 10303 | Centillion | Thousand quinquagintillion | Quinquagintilliard | 1000100+1 | 100000050.5 |
| ... | ... | ... | ... | ... | |
| 10360 | Cennovemdecillion | Sexagintillion | 1000119+1 | 100000060 | |
| 10420 | Cennovemtrigintillion | Septuagintillion | 1000139+1 | 100000070 | |
| 10480 | Cennovemquinquagintillion | Octogintillion | 1000159+1 | 100000080 | |
| 10540 | Cennovemseptuagintillion | Nonagintillion | 1000179+1 | 100000090 | |
| 10600 | Cennovemnonagintillion | Centillion | 1000199+1 | 1000000100 | |
| 10603 | Ducentillion | Thousand centillion | Centilliard | 1000200+1 | 1000000100.5 |
| 10606 | Killcentillion | 10 Thousand centillion | 1000201+1 | 1000000101 | |
There is no consistent and widely accepted way to extend cardinals beyond centillion (centilliard).
{{anchor|Myriad system}} Myriad, Octad, and -yllion systems
| Value | Myriad System Name | Octad System Name | Chinese Myriad Scale | Chinese Long Scale | Knuth-proposed System Name | Knuth-proposed System Notation |
|---|---|---|---|---|---|---|
| 100 | One | One | 一 | 一 | One | 1 |
| 101 | Ten | Ten | 十 | 十 | Ten | 10 |
| 102 | Hundred | Hundred | 百 | 百 | Hundred | 100 |
| 103 | Thousand | Thousand | 千 | 千 | Ten hundred | 1000 |
| 104 | Myriad | Myriad | 萬 (万) | 萬 (万) | Myriad | 1,0000 |
| 105 | Ten myriad | Ten myriad | 十萬 (十万) | 十萬 (十万) | Ten myriad | 10,0000 |
| 106 | Hundred myriad | Hundred myriad | 百萬 (百万) | 百萬 (百万) | Hundred myriad | 100,0000 |
| 107 | Thousand myriad | Thousand myriad | 千萬 (千万) | 千萬 (千万) | Ten hundred myriad | 1000,0000 |
| 108 | Second Myriad | Octad | 億 (亿) | 億 (亿) | Myllion | 1;0000,0000 |
| 1012 | Third myriad | Myriad Octad | 兆 | 萬億 | Myriad myllion | 1,0000;0000,0000 |
| 1016 | Fourth myriad | Second octad | 京 | 兆 | Byllion | 1:0000,0000;0000,0000 |
| 1020 | Fifth myriad | Myriad second octad | 垓 | 萬兆 | ||
| 1024 | Sixth myriad | Third octad | 秭 | 億兆 | Myllion byllion | 1;0000,0000:0000,0000;0000,0000 |
| 1028 | Seventh myriad | Myriad third octad | 穰 | 萬億兆 | ||
| 1032 | Eighth myriad | Fourth octad | 溝 (沟) | 京 | Tryllion | 1'0000,0000;0000,0000:0000,0000;0000,0000 |
| 1036 | Ninth myriad | Myriad fourth octad | 澗 (涧) | 萬京 | ||
| 1040 | Tenth myriad | Fifth octad | 正 | 億京 | ||
| 1044 | Eleventh myriad | Myriad fifth octad | 載 (载) | 萬億京 | ||
| 1048 | Twelveth myriad | Sixth octad | 極 (极) (in China and in Japan) | 兆京 | ||
| 1052 | Thirteenth myriad | Myriad sixth octad | 恆河沙 (恒河沙) (in China) | 萬兆京 | ||
| 1056 | Fourteenth myriad | Seventh octad | 阿僧祇 (in China); 恆河沙 (恒河沙) (in Japan) | 億兆京 | ||
| 1060 | Fifteenth myriad | Myriad seventh octad | 那由他, 那由多 (in China) | 萬億兆京 | ||
| 1064 | Sixteenth myriad | Eighth octad | 不可思議 (不可思议) (in China), 阿僧祇 (in Japan) | 垓 | Quadryllion | 1"0000,0000;0000,0000:0000,0000;0000,0000'0000,0000;0000,0000:0000,0000;0000,0000 |
| 1068 | Seventeenth myriad | Myriad eighth octad | 無量大数 (in China) | 萬垓 | ||
| 1072 | Eighteenth myriad | Nineth octad | 那由他, 那由多 (in Japan) | 億垓 | ||
| 1080 | Twentieth myriad | Tenth octad | 不可思議 (in Japan) | 兆垓 | ||
| 1088 | Twenty-second myriad | Eleventh Octad | 無量大数 (in Japan) | 億兆垓 | ||
| 10128 | 秭 | Quintyllion | ||||
| 10256 | 穰 | Sextyllion | ||||
| 10512 | 溝 (沟) | Septyllion | ||||
| 101,024 | 澗 (涧) | Octyllion | ||||
| 102,048 | 正 | Nonyllion | ||||
| 104,096 | 載 (载) | Decyllion | ||||
| 108,192 | 極 (极) | Undecyllion | ||||
| 1016,384 | Duodecyllion | |||||
| 1032,768 | Tredecyllion | |||||
| 1065,536 | Quattuordecyllion | |||||
| 10131,072 | Quindecyllion | |||||
| 10262,144 | Sexdecyllion | |||||
| 10524,288 | Septendecyllion | |||||
| 101,048,576 | Octodecyllion | |||||
| 102,097,152 | Novemdecyllion | |||||
| 104,194,304 | Vigintyllion | |||||
| 10232 | Trigintyllion | |||||
| 10242 | Quadragintyllion | |||||
| 10252 | Quinquagintyllion | |||||
| 10262 | Sexagintyllion | |||||
| 10272 | Septuagintyllion | |||||
| 10282 | Octogintyllion | |||||
| 10292 | Nonagintyllion | |||||
| 102102 | Centyllion | |||||
| 1021,002 | Millyllion | |||||
| 10210,002 | Myryllion | |||||
SI prefixes for powers of 10
| Value | 1000m | SI prefix | Name | Binary prefix | 1024m = 210m | Value |
|---|---|---|---|---|---|---|
| {{gaps|1|000}} | 10001 | k | Kilo | Ki | 10241 | 1 024 |
| {{gaps|1|000|000}} | 10002 | M | Mega | Mi | 10242 | 1 048 576 |
| {{gaps|1|000|000|000}} | 10003 | G | Giga | Gi | 10243 | 1 073 741 824 |
| {{gaps|1|000|000|000|000}} | 10004 | T | Tera | Ti | 10244 | 1 099 511 627 776 |
| {{gaps|1|000|000|000|000|000}} | 10005 | P | Peta | Pi | 10245 | 1 125 899 906 842 624 |
| {{gaps|1|000|000|000|000|000|000}} | 10006 | E | Exa | Ei | 10246 | 1 152 921 504 606 846 976 |
| {{gaps|1|000|000|000|000|000|000|000}} | 10007 | Z | Zetta | Zi | 10247 | 1 180 591 620 717 411 303 424 |
| {{gaps|1|000|000|000|000|000|000|000|000}} | 10008 | Y | Yotta | Yi | 10248 | 1 208 925 819 614 629 174 706 176 |
{{anchor|Fractional numbers}} Fractional numbers
{{See also|Fraction (mathematics)#Vocabulary|English numerals#Fractions and decimals}}This is a table of English names for non-negative rational numbers less than or equal to 1. It also lists alternative names, but there is no widespread convention for the names of extremely small positive numbers.
Keep in mind that rational numbers like 0.12 can be represented in infinitely many ways, e.g. zero-point-one-two (0.12), twelve percent (12%), three twenty-fifths ({{sfrac|3|25}}), nine seventy-fifths ({{sfrac|9|75}}), six fiftieths ({{sfrac|6|50}}), twelve hundredths ({{sfrac|12|100}}), twenty-four two-hundredths ({{sfrac|24|200}}), etc.
| Value | Fraction | Common names | Alternative names |
|---|---|---|---|
| 1 | {{sfrac|1|1}} | One | 0.999..., Unity |
| 0.9 | {{sfrac|9|10}} | Nine tenths, [zero] point nine | |
| 0.8 | {{sfrac|4|5}} | Four fifths, eight tenths, [zero] point eight | |
| 0.7 | {{sfrac|7|10}} | Seven tenths, [zero] point seven | |
| 0.6 | {{sfrac|3|5}} | Three fifths, six tenths, [zero] point six | |
| 0.5 | {{sfrac|1|2}} | One half, five tenths, [zero] point five | |
| 0.4 | {{sfrac|2|5}} | Two fifths, four tenths, [zero] point four | |
| 0.333|333...}} | {{sfrac|1|3}} | One third | |
| 0.3 | {{sfrac|3|10}} | Three tenths, [zero] point three | |
| 0.25 | {{sfrac|1|4}} | One quarter, one fourth, twenty-five hundredths, [zero] point two five | |
| 0.2 | {{sfrac|1|5}} | One fifth, two tenths, [zero] point two | |
| 0.166|666...}} | {{sfrac|1|6}} | One sixth | |
| 0.142|857|142|857...}} | {{sfrac|1|7}} | One seventh | |
| 0.125 | {{sfrac|1|8}} | One eighth, one-hundred-[and-]twenty-five thousandths, [zero] point one two five | |
| 0.111|111...}} | {{sfrac|1|9}} | One ninth | |
| 0.1 | {{sfrac|1|10}} | One tenth, [zero] point one | One perdecime, one perdime |
| 0.090|909...}} | {{sfrac|1|11}} | One eleventh | |
| 0.09 | {{sfrac|9|100}} | Nine hundredths, [zero] point zero nine | |
| 0.083|333...}} | {{sfrac|1|12}} | One twelfth | |
| 0.08 | {{sfrac|2|25}} | Two twenty-fifths, eight hundredths, [zero] point zero eight | |
| 0.0625 | {{sfrac|1|16}} | One sixteenth, six-hundred-[and-]twenty-five ten-thousandths, [zero] point zero six two five | |
| 0.05 | {{sfrac|1|20}} | One twentieth, five hundredths, [zero] point zero five | |
| 0.047|619|047|619...}} | {{sfrac|1|21}} | One twenty-first | |
| 0.045|454|545...}} | {{sfrac|1|22}} | One twenty-second | |
| 0.043|478|260|869|565|217|391|304|347...}} | {{sfrac|1|23}} | One twenty-third | |
| 0.041|666...}} | {{sfrac|1|24}} | One twenty-fourth | |
| 0.033|333...}} | {{sfrac|1|30}} | One thirtieth | |
| 0.03125 | {{sfrac|1|32}} | One thirty-second, thirty one-hundred [and] twenty five hundred-thousandths, [zero] point zero three one two five | |
| 0.016|666...}} | {{sfrac|1|60}} | One sixtieth | |
| 0.015625 | {{sfrac|1|64}} | One sixty-fourth, ten thousand fifty six-hundred [and] twenty-five millionths, [zero] point zero one five six two five | |
| 0.012|345|679|012|345|679...}} | {{sfrac|1|81}} | One eighty-first | |
| 0.01 | {{sfrac|1|100}} | One hundredth, [zero] point zero one | One percent |
| 0.001 | {{sfrac|1|1000}} | One thousandth, [zero] point zero zero one | One permille |
| 0.000|277|777...}} | {{sfrac|1|3600}} | One thirty-six hundredth | |
| 0.0001 | {{sfrac|1|{{gaps|10|000}}}} | One ten-thousandth, [zero] point zero zero zero one | One myriadth, one permyria, one permyriad, one basis point |
| 0.000|01}} | {{sfrac|1|{{gaps|100|000}}}} | One hundred-thousandth, [zero] point zero zero zero zero one | One lakhth, one perlakh |
| 0.000|001}} | {{sfrac|1|{{gaps|1|000|000}}}} | One millionth, [zero] point zero zero zero zero zero one | One ppm |
| 0.000|000|1}} | {{sfrac|1|{{gaps|10|000|000}}}} | One ten-millionth | One crorth, one percrore |
| 0.000|000|01}} | {{sfrac|1|{{gaps|100|000|000}}}} | One hundred-millionth | |
| 0.000|000|001}} | {{sfrac|1|{{gaps|1|000|000|000}}}} | One billionth (in some dialects) | One ppb |
| 0 | {{sfrac|0|1}} | Zero | Nil |
Irrational and suspected irrational numbers
{{main|Irrational number}}Algebraic numbers
{{main|Algebraic number}}| Expression | Approximate value | Notes |
|---|---|---|
| {{sfrac|{{sqrt|3}}|4}} | 0.433012701892219323381861585376}} | Area of an equilateral triangle with side length 1. |
| {{sfrac|{{sqrt|5}} − 1|2}} | 0.618033988749894848204586834366}} | Golden ratio conjugate Φ, reciprocal of and one less than the golden ratio. |
| {{sfrac|{{sqrt|3}}|2}} | 0.866025403784438646763723170753}} | Height of an equilateral triangle with side length 1. |
| {{radic|2|12}} | 1.059463094359295264561825294946}} | Twelfth root of two. Proportion between the frequencies of adjacent semitones in the equal temperament scale. |
| {{sfrac|3{{sqrt|2}}|4}} | 1.060660171779821286601266543157}} | The size of the cube that satisfies Prince Rupert's cube. |
| {{radic|2|3}} | 1.259921049894873164767210607278}} | Cube root of two. Length of the edge of a cube with volume two. See doubling the cube for the significance of this number. |
| — | 1.303577269034296391257099112153}} | Conway's constant, defined as the unique positive real root of a certain polynomial of degree 71. |
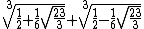 | 1.324717957244746025960908854478}} | x{{sup>3}} = x + 1. |
| {{sqrt|2}} | 1.414213562373095048801688724210}} | 2}} = 2 sin 45° = 2 cos 45° Square root of two a.k.a. Pythagoras' constant. Ratio of diagonal to side length in a square. Proportion between the sides of paper sizes in the ISO 216 series (originally DIN 476 series). |
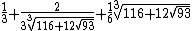 | 1.465571231876768026656731225220}} | The supergolden ratio, the only real solution of 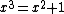 . Also the limit to the ratio between subsequent numbers in the binary Look-and-say sequence. . Also the limit to the ratio between subsequent numbers in the binary Look-and-say sequence. |
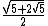 | 1.538841768587626701285145288018}} | Altitude of a regular pentagon with side length 1. |
| {{sfrac|{{sqrt|17}} − 1|2}} | 1.561552812808830274910704927987}} | The Triangular root of 2. |
| {{sfrac|{{sqrt|5}} + 1|2}} | 1.618033988749894848204586834366}} | x{{sup>2}} = x + 1. |
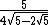 | 1.720477400588966922759011977389}} | Area of a regular pentagon with side length 1. |
| {{sqrt|3}} | 1.732050807568877293527446341506}} | 3}} = 2 sin 60° = 2 cos 30° Square root of three a.k.a. the measure of the fish. Length of the space diagonal of a cube with edge length 1. Length of the diagonal of a 1 × {{sqrt|2}} rectangle. Altitude of an equilateral triangle with side length 2. Altitude of a regular hexagon with side length 1 and diagonal length 2. |
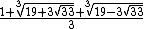 | 1.839286755214161132551852564653}} | The Tribonacci constant. Appears in the volume and coordinates of the snub cube and some related polyhedra. It satisfies the equation x + x−3 = 2. |
| {{sqrt|5}} | 2.236067977499789696409173668731}} | Length of the diagonal of a 1 × 2 rectangle. Length of the diagonal of a {{sqrt>2}} × {{sqrt|3}} rectangle. Length of the space diagonal of a 1 × {{sqrt|2}} × {{sqrt|2}} rectangular box. |
| {{sqrt|2}} + 1 | 2.414213562373095048801688724210}} | S}}), the larger of the two real roots of x{{sup|2}} = 2x + 1. Altitude of a regular octagon with side length 1. |
| {{sqrt|6}} | 2.449489742783178098197284074706}} | 2}} · {{sqrt|3}} = area of a {{sqrt|2}} × {{sqrt|3}} rectangle. Length of the space diagonal of a 1 × 1 × 2 rectangular box. Length of the diagonal of a 1 × {{sqrt|5}} rectangle. Length of the diagonal of a 2 × {{sqrt|2}} rectangle. Length of the diagonal of a square with side length {{sqrt|3}}. |
| {{sfrac|3{{sqrt|3}}|2}} | 2.598076113533159402911695122588}} | Area of a regular hexagon with side length 1. |
| {{sqrt|7}} | 2.645751311064590590501615753639}} | 2}} rectangular box. Length of the diagonal of a 1 × {{sqrt|6}} rectangle. Length of the diagonal of a 2 × {{sqrt|3}} rectangle. Length of the diagonal of a {{sqrt|2}} × {{sqrt|5}} rectangle. |
| {{sqrt|8}} | 2.828427124746190097603377448419}} | 2}} Volume of a cube with edge length {{sqrt|2}}. Length of the diagonal of a square with side length 2. Length of the diagonal of a 1 × {{sqrt|7}} rectangle. Length of the diagonal of a {{sqrt|2}} × {{sqrt|6}} rectangle. Length of the diagonal of a {{sqrt|3}} × {{sqrt|5}} rectangle. |
| {{sqrt|10}} | 3.162277660168379331998893544433}} | 2}} · {{sqrt|5}} = area of a {{sqrt|2}} × {{sqrt|5}} rectangle. Length of the diagonal of a 1 × 3 rectangle. Length of the diagonal of a 2 × {{sqrt|6}} rectangle. Length of the diagonal of a {{sqrt|3}} × {{sqrt|7}} rectangle. Length of the diagonal of a square with side length {{sqrt|5}}. |
| {{sqrt|11}} | 3.316624790355399849114932736671}} | Length of the diagonal of a 1 × {{sqrt>10}} rectangle. Length of the diagonal of a 2 × {{sqrt|7}} rectangle. Length of the diagonal of a 3 × {{sqrt|2}} rectangle. Length of the diagonal of a {{sqrt|3}} × {{sqrt|8}} rectangle. Length of the diagonal of a {{sqrt|5}} × {{sqrt|6}} rectangle. |
| {{sqrt|12}} | 3.464101615137754587054892683012}} | 3}} Length of the space diagonal of a cube with edge length 2. Length of the diagonal of a 1 × {{sqrt|11}} rectangle. Length of the diagonal of a 2 × {{sqrt|8}} rectangle. Length of the diagonal of a 3 × {{sqrt|3}} rectangle. Length of the diagonal of a {{sqrt|2}} × {{sqrt|10}} rectangle. Length of the diagonal of a {{sqrt|5}} × {{sqrt|7}} rectangle. Length of the diagonal of a square with side length {{sqrt|6}}. |
Transcendental numbers
{{main|Transcendental number}}- (−1)i = e−{{pi}} = {{val|0.0432139183}}...
- Liouville constant: c = {{val|0.110001000000000000000001000}}...
- Champernowne constant: C10 = {{val|0.12345678910111213141516}}...
- ii = {{sqrt|e{{sup|−{{pi}}}}}} = {{val|0.207879576}}...
- {{sfrac|1|{{pi}}}} = {{val|0.318309886183790671537767526745028724068919291480}}...[7]
- {{sfrac|1|e}} = {{val|0.367879441171442321595523770161460867445811131031}}...[7]
- Prouhet–Thue–Morse constant: {{mvar|τ}} = {{val|0.412454033640}}...
- log10 e = {{val|0.434294481903251827651128918916605082294397005803}}...[7]
- Omega constant: Ω = {{val|0.5671432904097838729999686622}}...
- Cahen's constant: c = {{val|0.64341054629}}...
- ln 2: {{val|0.693147180559945309417232121458}}...
- {{sfrac|{{pi}}|{{sqrt|18}}}} = 0.7404... the maximum density of sphere packing in three dimensional Euclidean space according to the Kepler conjecture[8]
- Gauss's constant: G = {{val|0.8346268}}...
- {{sfrac|{{pi}}|{{sqrt|12}}}} = 0.9068..., the fraction of the plane covered by the densest possible circle packing[9]
- ei + e−i = 2 cos 1 = {{val|1.08060461}}...
- {{sfrac|{{pi}}{{sup|4}}|90}} = ζ(4) = {{val|1.082323}}...[10]
- {{sqrt|2}}{{sub|s}}: {{val|1.559610469}}...[11]
- log2 3: {{val|1.584962501}}... (the logarithm of any positive integer to any integer base greater than 1 is either rational or transcendental)
- Gaussian integral: {{sqrt|{{pi}}}} = {{val|1.772453850905516}}...
- Komornik–Loreti constant: q = {{val|1.787231650}}...
- Universal parabolic constant: P2 = {{val|2.29558714939}}...
- Gelfond–Schneider constant: 2{{sup|{{sqrt|2}}}} = {{val|2.665144143}}...
- e = {{val|2.718281828459045235360287471352662497757247}}...
- {{pi}} = {{val|3.141592653589793238462643383279502884197169399375}}...
- {{radic|i|i}} = {{sqrt|e{{sup|{{pi}}}}}} = {{val|4.810477381}}...
- Tau, or 2{{pi}}: {{mvar|τ}} = {{val|6.283185307179586476925286766559}}..., The ratio of the circumference to a radius, and the number of radians in a complete circle[12][13]
- Gelfond's constant: {{val|23.14069263277925}}...
- Ramanujan's constant: e{{sup|{{pi}}{{sqrt|163}}}} = {{val|262537412640768743.99999999999925}}...
Suspected transcendentals
These are irrational numbers that are thought to be, but have not yet been proved to be, transcendental.
- Z(1): {{val|-0.736305462867317734677899828925614672}}...
- Heath-Brown–Moroz constant: C = {{val|0.001317641}}...
- Kepler–Bouwkamp constant: {{val|0.1149420448}}...
- MRB constant: {{val|0.187859}}...
- Meissel–Mertens constant: M = {{val|0.2614972128476427837554268386086958590516}}...
- Bernstein's constant: β = {{val|0.2801694990}}...
- Strongly carefree constant: {{val|0.286747}}...[14]
- Gauss–Kuzmin–Wirsing constant: λ1 = {{val|0.3036630029}}...[15]
- Hafner–Sarnak–McCurley constant: {{val|0.3532363719}}...
- Artin's constant: {{val|0.3739558136}}...
- Prime constant: ρ = {{val|0.414682509851111660248109622}}...
- Carefree constant: {{val|0.428249}}...[16]
- S(1): {{val|0.438259147390354766076756696625152}}...
- F(1): {{val|0.538079506912768419136387420407556}}...
- Stephens' constant: {{val|0.575959}}...[17]
- Euler–Mascheroni constant: γ = {{val|0.577215664901532860606512090082}}...
- Golomb–Dickman constant: λ = {{val|0.62432998854355087099293638310083724}}...
- Twin prime constant: C2 = {{val|0.660161815846869573927812110014}}...
- Copeland–Erdős constant: {{val|0.235711131719232931374143}}...
- Feller–Tornier constant: {{val|0.661317}}...[18]
- Laplace limit: ε = {{val|0.6627434193}}...[19]
- Taniguchi's constant: {{val|0.678234}}...[20]
- Continued Fraction Constant: C = {{val|0.697774657964007982006790592551}}...[21]
- Embree–Trefethen constant: β = {{val|0.70258}}...
- Sarnak's constant: {{val|0.723648}}...[22]
- Landau–Ramanujan constant: {{val|0.76422365358922066299069873125}}...
- C(1): {{val|0.77989340037682282947420641365}}...
- {{sfrac|1|ζ(3)}} = {{val|0.831907}}..., the probability that three random numbers have no common factor greater than 1.[8]
- Brun's constant for prime quadruplets: B2 = {{val|0.8705883800}}...
- Quadratic class number constant: {{val|0.881513}}...[23]
- Catalan's constant: G = {{val|0.915965594177219015054603514932384110774}}...
- Viswanath's constant: σ(1) = {{val|1.1319882487943}}...
- Khinchin–Lévy constant: {{val|1.1865691104}}...[24]
- ζ(3) = {{val|1.202056903159594285399738161511449990764986292}}..., also known as Apéry's constant, known to be irrational, but not known whether or not it is transcendental.[25]
- Vardi's constant: E = {{val|1.264084735305}}...
- Glaisher–Kinkelin constant: A = {{val|1.28242712}}...
- Mills' constant: A = {{val|1.30637788386308069046}}...
- Totient summatory constant: {{val|1.339784}}...[26]
- Ramanujan–Soldner constant: μ = {{val|1.451369234883381050283968485892027449493}}...
- Backhouse's constant: {{val|1.456074948}}...
- Favard constant: K1 = {{val|1.57079633}}...
- Erdős–Borwein constant: E = {{val|1.606695152415291763}}...
- Somos' quadratic recurrence constant: σ = {{val|1.661687949633594121296}}...
- Niven's constant: c = {{val|1.705211}}...
- Brun's constant: B2 = {{val|1.902160583104}}...
- Landau's totient constant: {{val|1.943596}}...[27]
- exp(−W{{sub|0}}(−ln({{radic|3|3}}))) = {{val|2.47805268028830}}..., the smaller solution to 3{{sup|x}} = x{{sup|3}} and what, when put to the root of itself, is equal to 3 put to the root of itself.[28]
- Second Feigenbaum constant: α = 2.5029...
- Sierpiński's constant: K = {{val|2.5849817595792532170658936}}...
- Barban's constant: {{val|2.596536}}...[29]
- Khinchin's constant: K0 = {{val|2.685452001}}...[30]
- Fransén–Robinson constant: F = {{val|2.8077702420}}...
- Murata's constant: {{val|2.826419}}...[31]
- Lévy's constant: γ = {{val|3.275822918721811159787681882}}...
- Reciprocal Fibonacci constant: ψ = {{val|3.359885666243177553172011302918927179688905133731}}...
- Van der Pauw's constant: {{sfrac|{{pi}}|ln 2}} = {{val|4.53236014182719380962}}...[32]
- First Feigenbaum constant: δ = 4.6692...
Numbers not known with high precision
- The constant in the Berry–Esseen Theorem: 0.4097 < C < 0.4748
- 2nd Landau's constant: 0.4330 < B < 0.472
- Bloch's constant: 0.4332 < B < 0.4719
- 1st Landau's constant: 0.5 < L < 0.5433
- 3rd Landau's constant: 0.5 < A ≤ 0.7853
- Grothendieck constant: 1.57 < k < 1.79
Hypercomplex numbers
{{main|Hypercomplex number}}Hypercomplex number is a traditional term for an element of a unital algebra over the field of real numbers.
Algebraic complex numbers
- Imaginary unit: i = {{sqrt|−1}}
- nth roots of unity: (ξ{{sub|n}}){{sup|k}} = cos (2{{pi}} {{sfrac|k|n}}) + i sin (2{{pi}} {{sfrac|k|n}}), while 0 ≤ k ≤ n−1, GCD(k, n) = 1
Other hypercomplex numbers
- The quaternions
- The octonions
- The sedenions
- The dual numbers (with an infinitesimal)
Transfinite numbers
{{main|Transfinite number}}Transfinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers, yet not necessarily absolutely infinite.
- Aleph-null: ℵ{{sub|0}}: the smallest infinite cardinal, and the cardinality of ℕ, the set of natural numbers
- Aleph-one: ℵ{{sub|1}}: the cardinality of ω1, the set of all countable ordinal numbers
- Beth-one: ℶ{{sub|1}} the cardinality of the continuum 2{{sup|ℵ{{sub|0}}}}
- ℭ or
 : the cardinality of the continuum 2{{sup|ℵ{{sub|0}}}}
: the cardinality of the continuum 2{{sup|ℵ{{sub|0}}}} - omega: ω, the smallest infinite ordinal
Numbers representing measured quantities
Various terms have arisen to describe commonly used measured quantities.
- Pair: 2 (the base of the binary numeral system)
- Dozen: 12 (the base of the duodecimal numeral system)
- Baker's dozen: 13
- Score: 20 (the base of the vigesimal numeral system)
- Gross: 144 (= 122)
- Great gross: 1728 (= 123)
Numbers representing physical quantities
Physical quantities that appear in the universe are often described using physical constants.
- Avogadro constant: N{{sub|A}} = {{val|6.0221417930e23}} mol−1
- Coulomb's constant: k{{sub|e}} = {{val|8.987551787368e9}} N·m2/C2 (m/F)
- Electronvolt: eV = {{val|1.60217648740e-19}} J
- Electron relative atomic mass: A{{sub|r}}(e) = {{val|0.0005485799094323}}...
- Fine structure constant: α = {{val|0.007297352537650}}...
- Gravitational constant: G = {{val|6.67384e−11}} N·(m/kg)2
- Molar mass constant: M{{sub|u}} = 0.001 kg/mol
- Planck constant: h = {{val|6.6260689633e-34}} J · s
- Rydberg constant: R{{sub|∞}} = {{val|10973731.56852773}} m−1
- Speed of light in vacuum: c = {{val|299792458}} m/s
- Stefan–Boltzmann constant: σ = {{val|5.670400e-8}} W · m−2 · K−4
Numbers without specific values
{{Main|Indefinite and fictitious numbers}}Many languages have words expressing indefinite and fictitious numbers—inexact terms of indefinite size, used for comic effect, for exaggeration, as placeholder names, or when precision is unnecessary or undesirable. One technical term for such words is "non-numerical vague quantifier".[33] Such words designed to indicate large quantities can be called "indefinite hyperbolic numerals".[34]
See also
{{col-begin}}{{col-break|width=33%}}- English-language numerals
- Floating point
- Fraction (mathematics)
- Integer sequence
- Interesting number paradox
- Large numbers
- List of mathematical constants
- List of numbers in various languages
- List of prime numbers
- List of types of numbers
- Mathematical constant
- Names of large numbers
- Names of small numbers
- Negative number
- Number prefix
- Numeral (linguistics)
- Orders of magnitude (numbers)
- Ordinal number
- The Penguin Dictionary of Curious and Interesting Numbers
- Power of two
- Powers of 10
- SI prefix
- Surreal number
- Table of prime factors
Notes
2. ^{{cite web|last1=Rouse|first1=Margaret|title=Mathematical Symbols|url=http://searchdatacenter.techtarget.com/definition/Mathematical-Symbols|accessdate=1 April 2015}}
3. ^{{cite web|url=http://www.merriam-webster.com/dictionary/86|title=Eighty-six – Definition of eighty-six by Merriam-Webster|work=merriam-webster.com|deadurl=no|archiveurl=https://web.archive.org/web/20130408004615/http://www.merriam-webster.com/dictionary/86|archivedate=2013-04-08|df=}}
4. ^{{cite web|url=http://mathworld.wolfram.com/Hardy-RamanujanNumber.html|title=Hardy–Ramanujan Number|first=Eric W.|last=Weisstein|publisher=|deadurl=no|archiveurl=https://web.archive.org/web/20040408221409/http://mathworld.wolfram.com/Hardy-RamanujanNumber.html|archivedate=2004-04-08|df=}}
5. ^1 2 {{cite web|url=https://books.google.com/books?id=cDkSAAAAYAAJ&pg=PA417&lpg=PA417&dq=%22long%20score%22%2021&source=bl&ots=uU-HfR9K0J&sig=YhXx-SlxYVF38x27a_X9Ia7ncR8&hl=en&ei=9vjSTbPvM8ezrAeys6jECQ&sa=X&oi=book_result&ct=result&resnum=1&ved=0CBgQ6AEwAA#v=onepage&q&f=false|title=The Shipmaster's Assistant, and Commercial Digest: Containing Information Useful to Merchants, Owners, and Masters of Ships |first=Joseph|last=Blunt|date=1 January 1837|publisher=E. & G.W. Blunt|via=Google Books}}
6. ^{{cite news |last=Ezard |first=John |date=2 Jan 2003 |title=Tolkien catches up with his hobbit |url=https://www.theguardian.com/uk/2003/jan/02/jrrtolkien.books |work=The Guardian |access-date=6 Apr 2018 }}
7. ^1 2 "The Penguin Dictionary of Curious and Interesting Numbers" by David Wells, page 27.
8. ^1 "The Penguin Dictionary of Curious and Interesting Numbers" by David Wells, page 29.
9. ^"The Penguin Dictionary of Curious and Interesting Numbers" by David Wells, page 30.
10. ^"The Penguin Dictionary of Curious and Interesting Numbers" by David Wells, page 33.
11. ^{{cite web|url=http://www.qbyte.org/puzzles/p029s.html|title=Nick's Mathematical Puzzles: Solution 29|publisher=|deadurl=no|archiveurl=https://web.archive.org/web/20111018184029/http://www.qbyte.org/puzzles/p029s.html|archivedate=2011-10-18|df=}}
12. ^"The Penguin Dictionary of Curious and Interesting Numbers" by David Wells, page 69
13. ^Sequence {{OEIS2C|A019692}}.
14. ^{{OEIS2C|A065473}}
15. ^{{mathworld|urlname=Gauss-Kuzmin-WirsingConstant|title=Gauss–Kuzmin–Wirsing Constant}}
16. ^{{OEIS2C|A065464}}
17. ^{{OEIS2C|A065478}}
18. ^{{OEIS2C|A065493}}
19. ^
20. ^{{OEIS2C|A175639}}
21. ^{{cite web|url=http://mathworld.wolfram.com/ContinuedFractionConstants.html|title=Continued Fraction Constant|first=Eric W.|last=Weisstein|publisher=Wolfram Research, Inc.|deadurl=no|archiveurl=https://web.archive.org/web/20111024094057/http://mathworld.wolfram.com/ContinuedFractionConstant.html|archivedate=2011-10-24|df=}}
22. ^{{OEIS2C|A065476}}
23. ^{{OEIS2C|A065465}}
24. ^
25. ^"The Penguin Dictionary of Curious and Interesting Numbers" by David Wells, page 33
26. ^{{OEIS2C|A065483}}
27. ^{{OEIS2C|A082695}}
28. ^{{OEIS2C|A166928}}
29. ^{{OEIS2C|A175640}}
30. ^
31. ^{{OEIS2C|A065485}}
32. ^{{OEIS2C|A163973}}
33. ^"Bags of Talent, a Touch of Panic, and a Bit of Luck: The Case of Non-Numerical Vague Quantifiers" from Linguista Pragensia, Nov. 2, 2010 {{webarchive|url=https://archive.is/20120731092211/http://versita.metapress.com/content/t98071387u726916/?p=1ad6a085630c432c94528c5548f5c2c4&pi=1 |date=2012-07-31 }}
34. ^[https://www.bostonglobe.com/ideas/2016/07/13/the-surprising-history-indefinite-hyperbolic-numerals/qYTKpkP9lyWVfItLXuTHdM/story.html Boston Globe, July 13, 2016: "The surprising history of indefinite hyperbolic numerals"]
Further reading
- Kingdom of Infinite Number: A Field Guide by Bryan Bunch, W.H. Freeman & Company, 2001. {{isbn|0-7167-4447-3}}
External links
- The Database of Number Correlations: 1 to 2000+
- What's Special About This Number? A Zoology of Numbers: from 0 to 500
- Name of a Number
- See how to write big numbers
- {{webarchive|url = https://web.archive.org/web/20101127194324/http://pages.prodigy.net/jhonig/bignum/indx.html|title = About big numbers|date = 27 November 2010}}
- Robert P. Munafo's Large Numbers page
- Different notations for big numbers – by Susan Stepney
- Names for Large Numbers, in How Many? A Dictionary of Units of Measurement by Russ Rowlett
- What's Special About This Number? (from 0 to 9999)
- Diptychophora molydocrossa
- Diptychophora moriokensis
- Diptychophora muscela
- Diptychophora muscella
- Diptychophora natalensis
- Diptychophora nymphocharis
- Diptychophora ochrophanes
- Diptychophora octavianella
- Diptychophora parorma
- Diptychophora pictella
- Diptychophora planetopa
- Diptychophora pogonias
- Diptychophora powelli
- Diptychophora praemialis
- Diptychophora pyrsophanes
- Diptychophora rusticula
- Diptychophora selenaea
- Diptychophora sericophthalma
- Diptychophora sinualis
- Diptychophora smithi
- Diptychophora stenura
- Diptychophora straminella
- Diptychophora straminiella
- Diptychophora strigatalis
- Diptychophora subazanalis