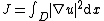1. Historical note

2. Motivating problems
    Shape of a membrane above an obstacle  Optimal stopping 

3. Formal statement

4. Alternative formulations
    Variational inequality  Least superharmonic function 

5. Regularity properties
    Optimal regularity  Level surfaces and the free boundary 

6. Generalizations

7. See also

8. Notes

9. Historical references

10. References

11. External links

The obstacle problem is a classic motivating example in the mathematical study of variational inequalities and free boundary problems. The problem is to find the equilibrium position of an elastic membrane whose boundary is held fixed, and which is constrained to lie above a given obstacle. It is deeply related to the study of minimal surfaces and the capacity of a set in potential theory as well. Applications include the study of fluid filtration in porous media, constrained heating, elasto-plasticity, optimal control, and financial mathematics.^[1]

The mathematical formulation of the problem is to seek minimizers of the Dirichlet energy functional,

in some domain where the functions represent the vertical displacement of the membrane. In addition to satisfying Dirichlet boundary conditions corresponding to the fixed boundary of the membrane, the functions are in addition constrained to be greater than some given obstacle function 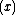. The solution breaks down into a region where the solution is equal to the obstacle function, known as the contact set, and a region where the solution is above the obstacle. The interface between the two regions is the free boundary.

In general, the solution is continuous and possesses Lipschitz continuous first derivatives, but that the solution is generally discontinuous in the second derivatives across the free boundary. The free boundary is characterized as a Hölder continuous surface except at certain singular points, which reside on a smooth manifold.

Historical note

Motivating problems

Shape of a membrane above an obstacle

The obstacle problem arises when one considers the shape taken by a soap film in a domain whose boundary position is fixed (see Plateau's problem), with the added constraint that the membrane is constrained to lie above some obstacle 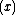in the interior of the domain as well.^[3] In this case, the energy functional to be minimized is the surface area integral, or

This problem can be linearized in the case of small perturbations by expanding the energy functional in terms of its Taylor series and taking the first term only, in which case the energy to be minimized is the standard Dirichlet energy

Optimal stopping

The obstacle problem also arises in control theory, specifically the question of finding the optimal stopping time for a stochastic process with payoff function .

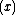In the simple case wherein the process is Brownian motion, and the process is forced to stop upon exiting the domain, the solution 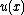of the obstacle problem can be characterized as the expected value of the payoff, starting the process at , if the optimal stopping strategy is followed. The stopping criterion is simply that one should stop upon reaching the contact set.^[4]

Formal statement

Suppose the following data is given:

1. an open bounded domain ⊂ ℝⁿ with smooth boundary
2. a smooth function on ∂ (the boundary of )
3. a smooth function 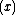defined on all of such that < , i.e. the restriction of 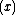to the boundary of (its trace) is less than .

Then consider the set

which is a closed convex subset of the Sobolev space of square integrable functions with square integrable weak first derivatives, containing precisely those functions with the desired boundary conditions which are also above the obstacle. The solution to the obstacle problem is the function which minimizes the energy integral

over all functions 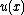belonging to ; the existence of such a minimizer is assured by considerations of Hilbert space theory.^[3][5]

Alternative formulations

Variational inequality

The obstacle problem can be reformulated as a standard problem in the theory of variational inequalities on Hilbert spaces. Seeking the energy minimizer in the set of suitable functions is equivalent to seeking

such that

where ⟨ . , . ⟩ : ℝⁿ × ℝⁿ → ℝ is the ordinary scalar product in the finite-dimensional real vector space ℝⁿ. This is a special case of the more general form for variational inequalities on Hilbert spaces, whose solutions are functions in some closed convex subset of the overall space, such that

for coercive, real-valued, bounded bilinear forms and bounded linear functionals .^[6]

Least superharmonic function

A variational argument shows that, away from the contact set, the solution to the obstacle problem is harmonic. A similar argument which restricts itself to variations that are positive shows that the solution is superharmonic on the contact set. Together, the two arguments imply that the solution is a superharmonic function.^[1]

In fact, an application of the maximum principle then shows that the solution to the obstacle problem is the least superharmonic function in the set of admissible functions.^[6]

Regularity properties

Optimal regularity

The solution to the obstacle problem has regularity, or bounded second derivatives, when the obstacle itself has these properties.^[7] More precisely, the solution's modulus of continuity and the modulus of continuity for its derivative are related to those of the obstacle.

1. If the obstacle has modulus of continuity , that is to say that , then the solution has modulus of continuity given by , where the constant depends only on the domain and not the obstacle.
2. If the obstacle's first derivative has modulus of continuity , then the solution's first derivative has modulus of continuity given by , where the constant again depends only on the domain.^&91;8&93;

Level surfaces and the free boundary

Subject to a degeneracy condition, level sets of the difference between the solution and the obstacle, for are surfaces. The free boundary, which is the boundary of the set where the solution meets the obstacle, is also except on a set of singular points, which are themselves either isolated or locally contained on a manifold.^[9]

Generalizations

The theory of the obstacle problem is extended to other divergence form uniformly elliptic operators,^[6] and their associated energy functionals. It can be generalized to degenerate elliptic operators as well.

The double obstacle problem, where the function is constrained to lie above one obstacle function and below another, is also of interest.

The Signorini problem is a variant of the obstacle problem, where the energy functional is minimized subject to a constraint which only lives on a surface of one lesser dimension, which includes the boundary obstacle problem, where the constraint operates on the boundary of the domain.

The parabolic, time-dependent cases of the obstacle problem and its variants are also objects of study.

See also

• Barrier option
• Minimal surface
• Variational inequality
• Signorini problem

Notes

Historical references

• {{Citation

}}. "Leonida Tonelli and the Pisa mathematical school" is a survey of the work of Tonelli in Pisa and his influence on the development of the school, presented at the International congress in occasion of the celebration of the centenary of birth of Mauro Picone and Leonida Tonelli (held in Rome on May 6–9, 1985). The Author was one of his pupils and, after his death, held his chair of mathematical analysis at the University of Pisa, becoming dean of the faculty of sciences and then rector: he exerted a strong positive influence on the development of the university.

References

• {{Citation

• {{Citation

}}. A set of lecture notes surveying "without too many precise details, the basic theory of probability, random differential equations and some applications", as the author himself states.

• {{Citation

}}.

• {{Citation

}}.

• {{Citation

• {{citation|last=Petrosyan|first=Arshak|last2=Shahgholian|first2=Henrik|last3=Uraltseva|first3=Nina|title=Regularity of Free Boundaries in Obstacle-Type Problems. Graduate Studies in Mathematics,|publisher=American Mathematical Society, Providence, RI|year=2012|isbn=0-8218-8794-7 }}

External links

• {{Citation

}}, delivered by the author at the Scuola Normale Superiore in 1998.

• Henry Collier (disambiguation)
• Henry Collin Minton
• Henry Combe Compton
• Henry (comic)
• Henry Commiskey
• Henry Commiskey, Sr.
• Henry Commiskey Sr.
• Henry Compton
• Henry Compton (actor)
• Henry Compton (disambiguation)
• Henry Conard
• Henry Condell (disambiguation)
• Henry Condell (musician)
• Henry Conger Pratt
• Henry Connor (disambiguation)
• Henry Constantine Wayne
• Henry Converse Atwill
• Henry Conway Belfield
• Henry Conyngham
• Henry Conyngham, 1st Earl Conyngham
• Henry Conyngham, 1st Marquess Conyngham KP GCH PC
• Henry Conyngham (disambiguation)
• Henry Conyngham, Earl of Mount Charles
• Henry Cook (aviator)
• Henry Cookson