假设检验的类型jiashe Jianyan de leixing
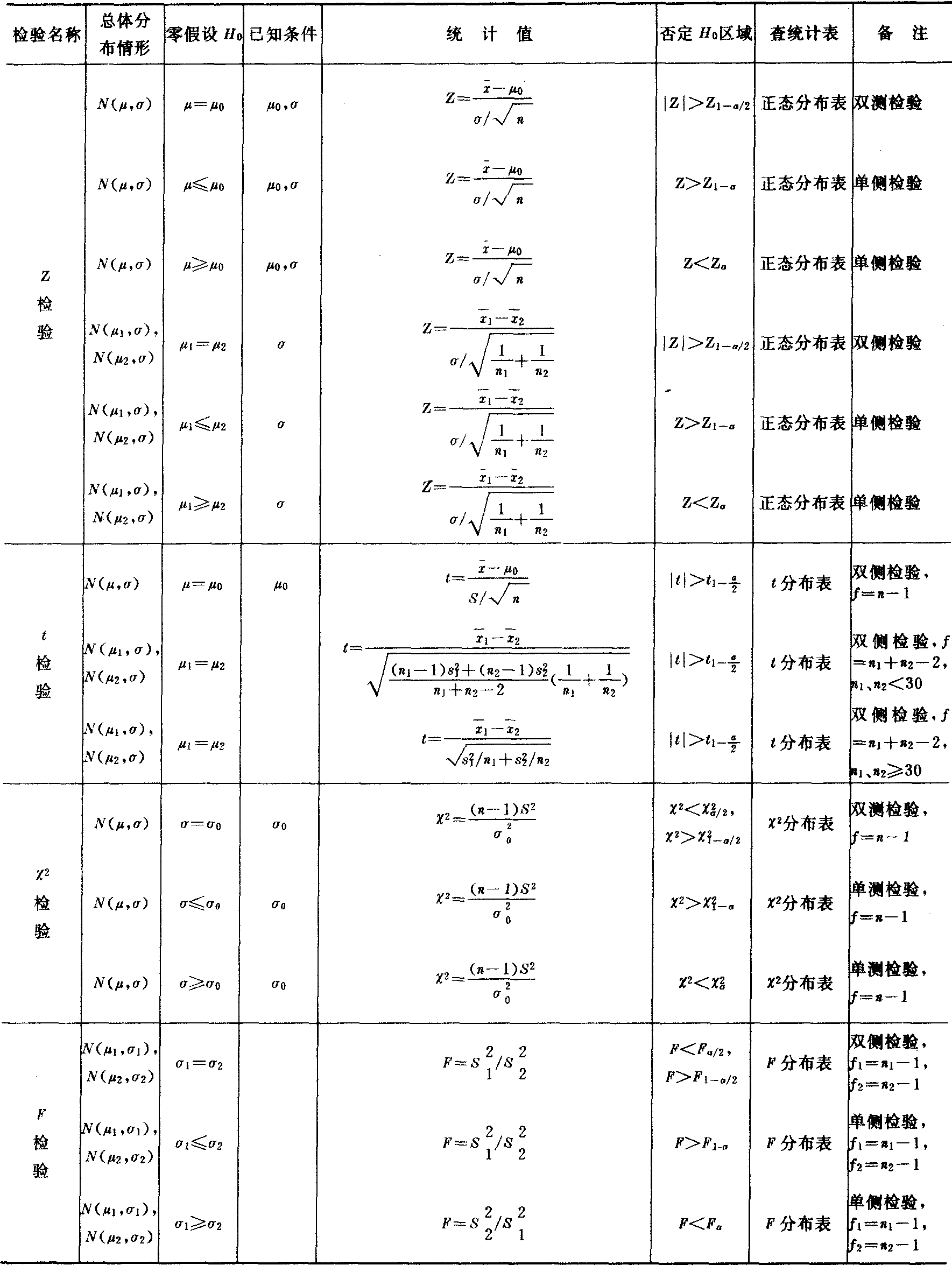
假设检验的内容十分丰富。对一个分布来说,主要想知道它的“中心”——平均数和“展形”——标准差的情况。因此把一个总体或两个总体情形下检验平均数和标准差的假设检验列表(见表1)。
下面举两个实例说明表1的应用。
[例1] 1989年某中学参加语文高考的46名学生的平均分为63. 5、标准差为11.8。已知该年全省语文科高考的平均分为65.5、标准差为13.4。问该校语文高考成绩能否作为总体的一个样本? (设a=0.05)
这是问,如果该校学生的语文高考成绩(平均分与标准差)与总体成绩无明显差别的话,则它可作为总体的一个样本。故零假设分别为H0:μ=65.5;H′0:δ2=13.42。
对前一假设而言,因μ0=65.5和δ0=13.4为已知,故统计值为Z= =-1.01。由正态分布表可知Z1-a/2=1.96,|Z|<1.96.故没有理由拒绝H0,即表明该校语文高考平均分与总体平均分之间没有明显的差别。
=-1.01。由正态分布表可知Z1-a/2=1.96,|Z|<1.96.故没有理由拒绝H0,即表明该校语文高考平均分与总体平均分之间没有明显的差别。
对后一假设而言,因σ0= 13.4为已知,故统计值为X2=(n-1)S2/σ02=(46-1)/13.42=34.9,据f=n-1=46-1=45及a=0.05,查x2分布表得:X2(45)0.025=65.38、X2(45)0.973=28.40,可知统计值34. 9并没有落在这一区间之外,故没有理由拒绝H0′。即表明该校语文高考的标准差与总体标准差之间也没有明显的差别。因此该校的语文高考成绩可作为总体的一个样本。
[例2] 为了对某门课的教学方法进行改革,某校对各方面情况相似的两个班进行了实验。甲班42人仍用教师面授的教学方法,乙班40人则采用讲授要点、学生研究讨论、定期作学习小结的教学方法。课程结束后用同一份试题对这两个班同时测验,结果甲班平均分78.5、标准差8.4,乙班平均分84、标准差10.5。问不同教法的教学效果是否明显?(a=0.05)
表1 独立样本的假设检验一览表(之一)
显然,这是两个平均数之差异的显著性检验,故H0:μ1=μ2。由于n1与n2均为大样本,故用公式
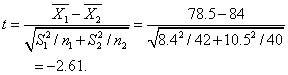 据f=42+40-2=80,及a=0.05,查t分布表得t(80)0.025=1.99。由于|t|=2.61>t(80)0.025=1.99,故拒绝H0,即表明这两个班的不同教法之间有明显的差别。从平均分来看即知,新教法明显优于旧教法。除表1列举之外,尚有一些独立样本的假设检验如下(见表2)。
据f=42+40-2=80,及a=0.05,查t分布表得t(80)0.025=1.99。由于|t|=2.61>t(80)0.025=1.99,故拒绝H0,即表明这两个班的不同教法之间有明显的差别。从平均分来看即知,新教法明显优于旧教法。除表1列举之外,尚有一些独立样本的假设检验如下(见表2)。表2 独立样本的假设检验一览表(之二)
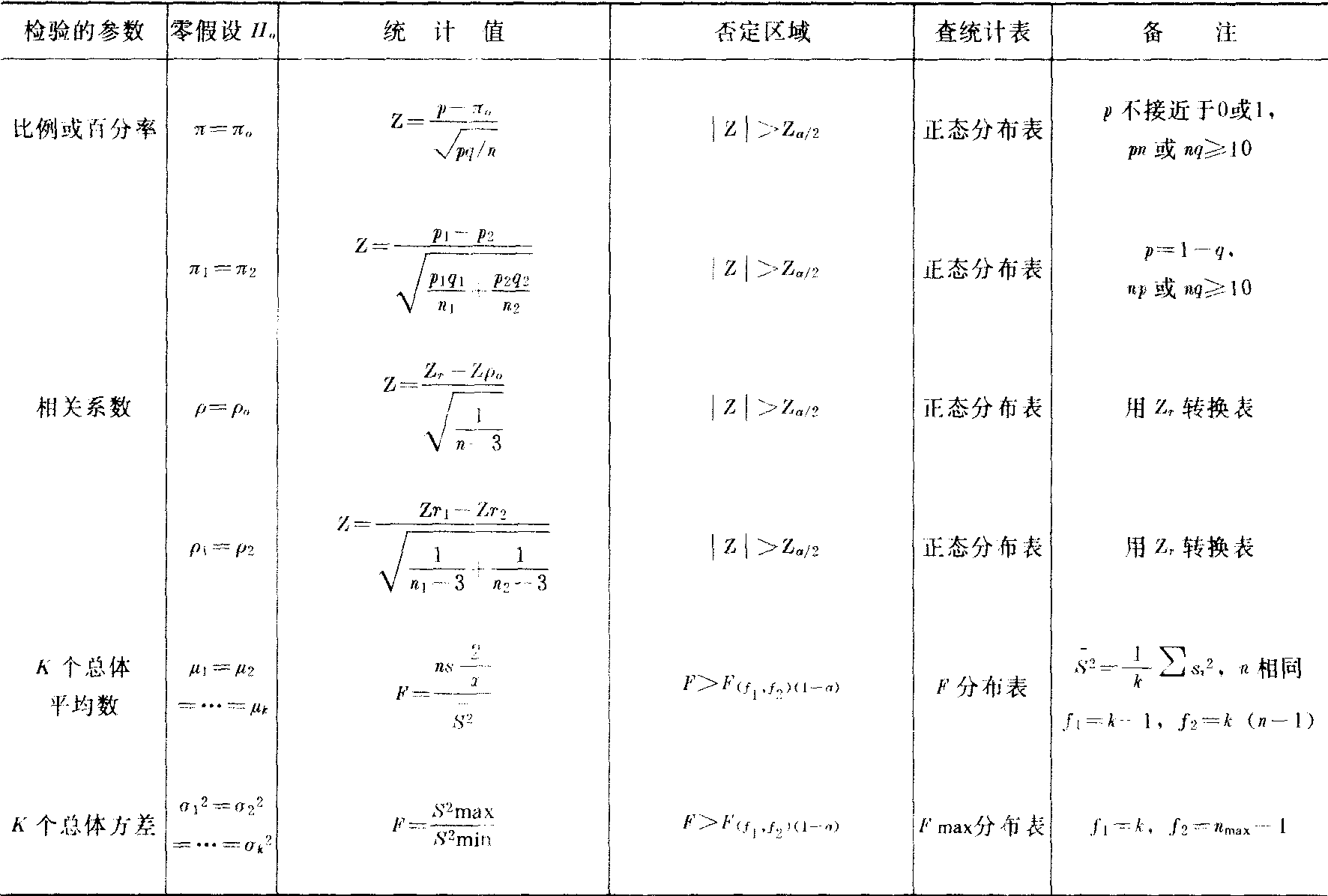
注:关于比例和相关系数,亦可用表1中类似的单侧检验。表1是对独立样本而言的。若样本之间存在着相关关系,则不宜使用表1进行假设检验而应使用下表。
表3 相关样本的假设检验一览表
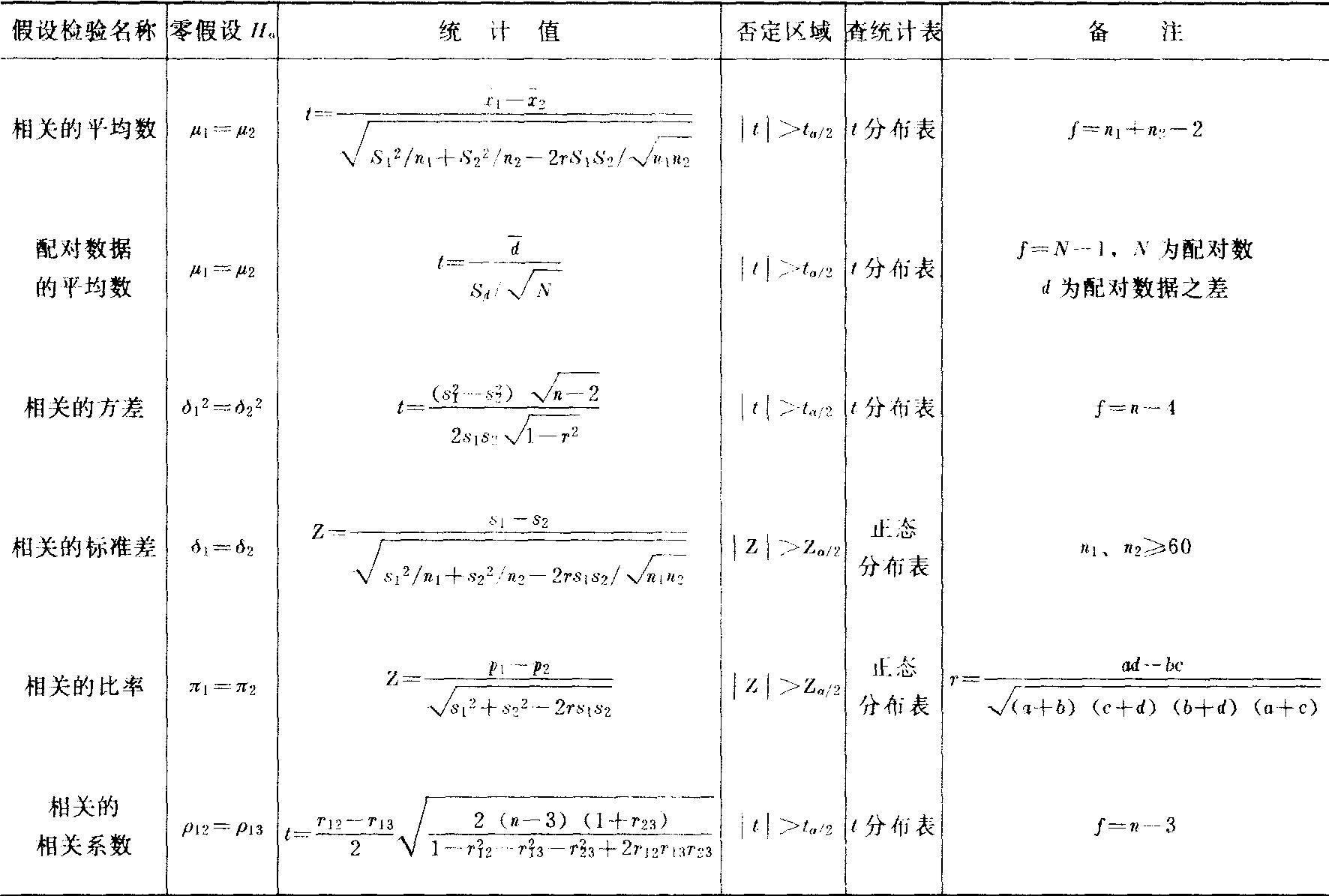
注:此处均为双侧检验,亦可用表1中类似的单侧检验。
[例3] 某中学初一班51名学生的学期初语文阅读测验成绩为
 =55、S1=8.3,学期末的类似阅读测验成绩为
=55、S1=8.3,学期末的类似阅读测验成绩为 =63、S2=9.5。已计出这两次测验成绩的相关系数为0.54,问学期末与学期初的阅读测验成绩之间是否有显著差异?
=63、S2=9.5。已计出这两次测验成绩的相关系数为0.54,问学期末与学期初的阅读测验成绩之间是否有显著差异?同一批考生接受两个类似的测验,则这批考生就是相关样本,因而这个问题属相关的平均数的检验,故H0:μ1=μ2,统计值为
 值代入后可得t=-6.64,据f=n1+n2-2=100及α=0.01在t分布表中查得t(100)0.005=2.625,可知|t|>t(100)0.005,故拒绝假设H0,即有理由认为期末阅读测验成绩极明显高于期初的阅读测验成绩。
值代入后可得t=-6.64,据f=n1+n2-2=100及α=0.01在t分布表中查得t(100)0.005=2.625,可知|t|>t(100)0.005,故拒绝假设H0,即有理由认为期末阅读测验成绩极明显高于期初的阅读测验成绩。