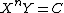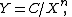- Example
- Software
- See also
- References
- Further reading
- External links
Lotka's law,[1] named after Alfred J. Lotka, is one of a variety of special applications of Zipf's law. It describes the frequency of publication by authors in any given field. It states that the number of authors making  contributions in a given period is a fraction of the number making a single contribution, following the formula
contributions in a given period is a fraction of the number making a single contribution, following the formula 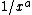 where a nearly always equals two, i.e., an approximate inverse-square law, where the number of authors publishing a certain number of articles is a fixed ratio to the number of authors publishing a single article. As the number of articles published increases, authors producing that many publications become less frequent. There are 1/4 as many authors publishing two articles within a specified time period as there are single-publication authors, 1/9 as many publishing three articles, 1/16 as many publishing four articles, etc. Though the law itself covers many disciplines, the actual ratios involved (as a function of 'a') are discipline-specific.
where a nearly always equals two, i.e., an approximate inverse-square law, where the number of authors publishing a certain number of articles is a fixed ratio to the number of authors publishing a single article. As the number of articles published increases, authors producing that many publications become less frequent. There are 1/4 as many authors publishing two articles within a specified time period as there are single-publication authors, 1/9 as many publishing three articles, 1/16 as many publishing four articles, etc. Though the law itself covers many disciplines, the actual ratios involved (as a function of 'a') are discipline-specific.
The general formula says:
or
where X is the number of publications, Y the relative frequency of authors with X publications, and n and  are constants depending on the specific field (
are constants depending on the specific field (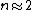 ).
).
Example
Say 100 authors write at least one article each over a specific period, we assume for this table that C=100 and n=2. Then the number of authors writing portions of any particular articles in that time period is describe as in the following table:
| Portion of articles written | Number of authors writing that number of articles |
|---|---|
| 10 | 100/102 = 1 |
| 9 | 100/92 ≈ 1 (1.23) |
| 8 | 100/82 ≈ 2 (1.56) |
| 7 | 100/72 ≈ 2 (2.04) |
| 6 | 100/62 ≈ 3 (2.77) |
| 5 | 100/52 = 4 |
| 4 | 100/42 ≈ 6 (6.25) |
| 3 | 100/32 ≈ 11 (11.111...) |
| 2 | 100/22 = 25 |
| 1 | 100 |
That would be a total of 294 articles with 155 writers with an average of 1.9 articles for each writer.
This is an empirical observation rather than a necessary result. This form of the law is as originally published and is sometimes referred to as the "discrete Lotka power function".[2]
Software
- Friedman, A. 2015. "The Power of Lotka’s Law Through the Eyes of R" The Romanian Statistical Review. Published by National Institute of Statistics. {{ISSN|1018-046X}}
- {{cite journal|title=LOTKA: A program to fit a power law distribution to observed frequency data|author=B Rousseau and R Rousseau|journal=Cybermetrics|volume=4|year=2000|issn=1137-5019}} - [https://web.archive.org/web/20100204183250/http://www.cindoc.csic.es/cybermetrics/articles/v4i1p4.html Software] to fit a Lotka power law distribution to observed frequency data.
See also
- Price's law
References
2. ^{{cite journal |last=Egghe |first=Leo |year=2005 |title=Relations between the continuous and the discrete Lotka power function|journal=Journal of the American Society for Information Science and Technology |volume=56 |issue=7 |pages=664–668 |doi=10.1002/asi.20157 }}
Further reading
- {{cite journal|title=Patterns of Productivity in the Finance Literature: A Study of the Bibliometric Distributions|author=Kee H. Chung and Raymond A. K. Cox|journal=Journal of Finance|volume=45|issue=1|date=March 1990|pages=301–309|doi=10.2307/2328824|jstor=2328824}} — Chung and Cox analyze a bibliometric regularity in finance literature, relating Lotka's law to the maxim that "the rich get richer and the poor get poorer", and equating it to the maxim that "success breeds success".
External links
- [https://archive.org/details/journalofwashin161926wash The Journal of the Washington Academy of Sciences, vol. 16]
- Route 327 (Nova Scotia)
- Route 327 (Virginia pre-1928)
- Route 328
- Route 328 (Florida)
- Route 329
- Route 329 (AR)
- Route 329 (Arkansas)
- Route 329 (Nova Scotia)
- Route 32A (Massachusetts)
- Route 32A (New England)
- Route 32A (New York)
- Route 32B (Florida)
- Route 32 (California)
- Route 32 (Connecticut)
- Route 32 (Connecticut 1920s)
- Route 32 (CT)
- Route 32 (Florida)
- Route 32 (Illinois)
- Route 32 (MA)
- Route 32 (Maryland)
- Route 32 (Massachusetts)
- Route 32 (Massachusetts 1920s)
- Route 32 (Missouri)
- Route 32 (MO)
- Route 32 (New England)