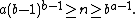- Definition
- Name
- Proof of finitude
- Tables of PDDIs
- References
- External links
A perfect digit-to-digit invariant (PDDI) (also known as a Munchausen number[1]) is a natural number that is equal to the sum of its digits each raised to the power of itself. In any base, there are only a finite number of Munchausen numbers. For example, in base 10 (decimal) there are only four: 0, 1, 3435 and 438579088.
Definition
A number 
in base 
with digits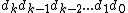 
(where each 
is an integer such that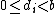 
) is a PDDI if and only if:
.
Although 00 is usually considered undefined, in the context of PDDIs it is usually taken to be equal to zero.[2][3]
An example of a PDDI is 3435, as 
.
0 and 1 are PDDIs in any base. Apart from 0 and 1 there are only two other PDDIs in the decimal system, 3435 and 438579088 {{OEIS|id=A046253}}. Note that 0 and 438579088 are PDDIs only when the convention that 
is used.
An example of a PDDI in another base is the quaternary number 313, or 55 in decimal, as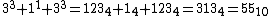 
.
Name
The term "Munchausen number" was coined by Dutch mathematician and software engineer Daan van Berkel in 2009.[4] Because each digit is raised by itself, this evokes the story of Baron Munchausen raising himself up by his own ponytail.[5] Narcissistic numbers follow a similar rule, but in the case of the narcissistics the powers of the digits are fixed, being raised to the power of the number of digits in the number. This is an additional explanation for the name, as Baron Münchhausen was famously narcissistic.[6]
Proof of finitude
{{unreferencedsection|date=February 2019}}There are finitely many PDDIs in any base. This can be proven as follows:
Let, where
is the number of digits in
is the largest possible digit in base
The expressionincreases exponentially with respect to
such that
There are finitely many natural numbers
Tables of PDDIs
Without considering numbers containing a (non-leading) zero, the following is an exhaustive list of PDDIs for integer bases up to 12 (excluding 1, a PDDI in all bases):[1]
| Base | PDDIs (in that base) | PDDIs (decimal representation) |
|---|---|---|
| 2 | 10 (requires 00 = 1) | 2 |
| 3 | 12, 22 | 5, 8 |
| 4 | 131, 313 | 29, 55 |
| 6 | 22352, 23452 | 3164, 3416 |
| 7 | 13454 | 3665 |
| 9 | 31, 156262, 1656547 | 28, 96446, 923362 |
| 10 | 3435 | 3435 |
| 12 | 3A67A54832 | 20017650854 |
When the convention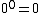 
is used the following numbers are also PDDIs (as well as 0, in all bases):
| Base | PDDIs (in that base) | PDDIs (decimal representation) |
|---|---|---|
| 4 | 130 | 28 |
| 5 | 103, 2024 | 28, 264 |
| 8 | 400, 401 | 256, 257 |
| 9 | 30, 1647063, 34664084 | 27, 917139, 16871323 |
| 10 | 438579088 | 438579088 |
References
2. ^Narcisstic Number, Harvey Heinz
3. ^{{cite book | last = Wells | first = David | title = The Penguin Dictionary of Curious and Interesting Numbers | publisher = Penguin | location = London | year = 1997 | page = 185 | isbn = 0-14-026149-4}}
4. ^Olry, Regis and Duane E. Haines. [https://books.google.com/books?id=h30pAgAAQBAJ&pg=PA136&dq=%22munchausen+number%22&hl=en&sa=X&ei=sx92Vby4G8mbyAT3noHYBA&ved=0CCsQ6AEwAQ#v=onepage&q=%22munchausen%20number%22&f=false "Historical and Literary Roots of Münchhausen Syndromes"], from Literature, Neurology, and Neuroscience: Neurological and Psychiatric Disorders, Stanley Finger, Francois Boller, Anne Stiles, eds. Elsevier, 2013. p.136.
5. ^Daan van Berkel, [https://arxiv.org/pdf/0911.3038v2.pdf On a curious property of 3435.]
6. ^{{cite book|last1=Parker|first1=Matt|title=Things to Make and Do in the Fourth Dimension|date=2014|publisher=Penguin UK|isbn=9781846147654|page=28|url=https://books.google.de/books?id=AOu2AwAAQBAJ&pg=PT28|accessdate=2 May 2015}}
External links
- {{cite web|last=Parker|first=Matt|title=3435|url=http://www.numberphile.com/videos/3435.html|work=Numberphile|publisher=Brady Haran}}