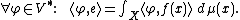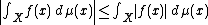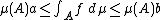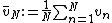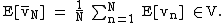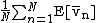“Pettis integral”的意思、由来-开放百科全书

词条

Pettis integral

释义

Definition
Properties
Mean value theorem Existence
Law of large numbers for Pettis-integrable random variables
See also
References

In mathematics, the Pettis integral or Gelfand–Pettis integral, named after Israel M. Gelfand and Billy James Pettis, extends the definition of the Lebesgue integral to vector-valued functions on a measure space, by exploiting duality. The integral was introduced by Gelfand for the case when the measure space is an interval with Lebesgue measure. The integral is also called the weak integral in contrast to the Bochner integral, which is the strong integral.

Definition

Let 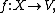where 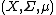is a measure space and is a topological vector space. Suppose that admits a dual space that separates points, e.g. is a Banach space or (more generally) a is locally-convex Hausdorff vector space. We write evaluation of a functional as duality pairing: .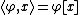

We say that is Pettis integrable if 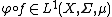for all 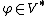and there exists a vector so that:

In this case, we call the Pettis integral of . Common notations for the Pettis integral include

Properties

An immediate consequence of the definition is that Pettis integrals are compatible with continuous, linear operators: If is and linear and continuous and 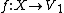is Pettis integrable, then is Pettis integrable as well and:

The standard estimate

for real- and complex-valued functions generalises to Pettis integrals in the following sense: For all continuous seminorms and all Pettis integrable

holds. The right hand side is the lower Lebesgue integral of a -valued function, i.e.

Taking a lower Lebesgue integral is necessary because the integrand may not be measurable. This follows from the Hahn-Banach theorem because for every vector there must be a continuous functional such that and . Applying this to it gives the result.

Mean value theorem

An important property is that the Pettis integral with respect to a finite measure is contained in the closure of the convex hull of the values scaled by the measure of the integration domain:

This is a consequence of the Hahn-Banach theorem and generalises the mean value theorem for integrals of real-valued functions: If then closed convex sets are simply intervals and for 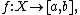the inequalities

hold.

Existence

If is finite-dimensional then is Pettis integrable if and only if each of 's coordinates is Lebesgue integrable.

If is Pettis integrable and 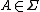is a measurable subset of , then and 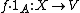are also Pettis integrable and

If is a topological space, 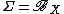its Borel--algebra, a Borel measure that assigns finite values to compact subsets, is quasi-complete (i.e. if every bounded Cauchy net converges) and if is continuous with compact support, then is Pettis integrable.

More generally: If is weakly measurable and there exists a compact, convex 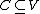and a null set 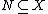such that 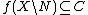, then is Pettis-integrable.

Law of large numbers for Pettis-integrable random variables

Let 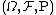be a probability space, and let be a topological vector space with a dual space that separates points. Let 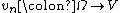be a sequence of Pettis-integrable random variables, and write 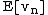for the Pettis integral of (over ). Note that 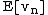is a (non-random) vector in , and is not a scalar value.

Let

denote the sample average. By linearity, 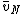is Pettis integrable, and

Suppose that the partial sums

converge absolutely in the topology of , in the sense that all rearrangements of the sum converge to a single vector . The weak law of large numbers implies that for every functional 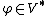. Consequently, in the weak topology on .

Without further assumptions, it is possible that does not converge to .{{Citation needed|date=October 2013}} To get strong convergence, more assumptions are necessary.{{Citation needed|date=October 2013}}

References

James K. Brooks, Representations of weak and strong integrals in Banach spaces, Proceedings of the National Academy of Sciences of the United States of America 63, 1969, 266–270. Fulltext {{MR|0274697}}
Israel M. Gel'fand, Sur un lemme de la théorie des espaces linéaires, Commun. Inst. Sci. Math. et Mecan., Univ. Kharkoff et Soc. Math. Kharkoff, IV. Ser. 13, 1936, 35–40 {{Zbl|0014.16202}}
Michel Talagrand, Pettis Integral and Measure Theory, Memoirs of the AMS no. 307 (1984) {{MR|0756174}}
{{springer|title=Pettis integral|id=p/p072490|first=V. I.|last=Sobolev}}

2 : Functional analysis|Integrals

随便看