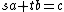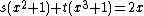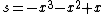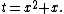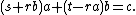“Polynomial Diophantine equation”的意思、由来-开放百科全书

词条

Polynomial Diophantine equation

释义

References

In mathematics, a polynomial Diophantine equation is an indeterminate polynomial equation for which one seeks solutions restricted to be polynomials in the indeterminate. A Diophantine equation, in general, is one where the solutions are restricted to some algebraic system, typically integers. (In another usage ) Diophantine refers to the Hellenistic mathematician of the 3rd century, Diophantus of Alexandria, who made initial studies of integer Diophantine equations.

An important type of polynomial Diophantine equations takes the form:

where a, b, and c are known polynomials, and we wish to solve for s and t.

A simple example (and a solution) is:

A necessary and sufficient condition for a polynomial Diophantine equation to have a solution is for c to be a multiple of the GCD of a and b. In the example above, the GCD of a and b was 1, so solutions would exist for any value of c.

Solutions to polynomial Diophantine equations are not unique. Any multiple of (say ) can be used to transform and into another solution :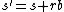

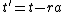Some polynomial Diophantine equations can be solved using the extended Euclidean algorithm, which works as well with polynomials as it does with integers.

References

{{cite book

| last = Bronstein
| first = Manuel
| title = Symbolic Integration I
| publisher = Springer
| date = 2005
| pages = 12–14
| isbn = 3-540-21493-3 }}

1 : Algebra

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。