- Causes
- Association studies
- Genomic control
- Demographic inference
- References
Population stratification (or population structure) is the presence of a systematic difference in allele frequencies between subpopulations in a population, possibly due to different ancestry, especially in the context of association studies.
Causes
The basic cause of population stratification is non-random mating between groups, often due to their physical separation (e.g., for populations of African and European descent) followed by genetic drift of allele frequencies in each group. In some contemporary populations there has been recent admixture between individuals from different populations, leading to populations in which ancestry is variable (as in African Americans). In some parts of the globe (e.g., in Europe), population structure is best modeled by isolation-by-distance, in which allele frequencies tend to vary smoothly with location.
Association studies
Population stratification can be a problem for association studies, such as case-control studies, where the association could be found due to the underlying structure of the population and not a disease associated locus. By analogy, one might imagine a scenario in which certain small beads are made out of a certain type of unique foam, and that children tend to choke on these beads; one might wrongly conclude that the foam material causes choking when in fact it is the small size of the beads. Also the real disease causing locus might not be found in the study if the locus is less prevalent in the population where the case subjects are chosen. For this reason, it was common in the 1990s to use family-based data where the effect of population stratification can easily be controlled for using methods such as the Transmission disequilibrium test (TDT). But if the structure is known or a putative structure is found, there are a number of possible ways to implement this structure in the association studies and thus
compensate for any population bias. Most contemporary genome-wide association studies take the view that the problem of population stratification is
manageable,[1] and that the logistic advantages of using unrelated cases and controls make these studies preferable to family-based association studies.
The two most widely used approaches to this problem include genomic control, which is a relatively nonparametric method for controlling the inflation of test statistics,[2] and structured association methods,[3] which use genetic information to estimate and control for population structure. Currently, the most widely used structured association method is Eigenstrat, developed by Alkes Price and colleagues.[4]
Genomic control
{{main|Genomic control}}The assumption of population homogeneity in association studies, especially case-control
studies, can easily be violated and can lead to both type I and type II errors. It is
therefore important for the models used in the study to compensate for the population
structure. The problem in case control studies is that if there is a genetic involvement in
the disease, the case population is more likely to be related than the individuals in the
control population. This means that the assumption of independence of observations is
violated. Often this will lead to an overestimation of the significance of an association
but it depends on the way the sample was chosen. If, coincidentally, there is a higher allele
frequency in a subpopulation of the cases, you will find association with any trait that is more prevalent
in the case population.[5] This kind of spurious association
increases as the sample population grows so the problem should be of special concern in
large scale association studies when loci only cause relatively small effects on the trait. A method that in some cases can compensate for the above described problems has been developed by Devlin and
Roeder (1999).[6] It uses both a frequentist and a Bayesian approach (the latter being
appropriate when dealing with a large number of candidate genes).
The frequentist way of correcting for population stratification works by using markers that are not linked with the trait in question to correct
for any inflation of the statistic caused by population stratification. The method was
first developed for binary traits but has since been generalized for quantitative ones.[7] For the binary one, which applies to finding genetic differences
between the case and control populations, Devlin and Roeder (1999) use Armitage's trend test
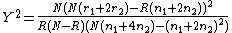
and the  test for allelic frequencies
test for allelic frequencies
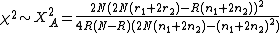
| Alleles | aa | Aa | AA | total |
|---|---|---|---|---|
| Case | r0 | r1 | r2 | R |
| Control | s0 | s1 | s2 | S |
| total | n0 | n1 | n2 | N |
If the population is in Hardy-Weinberg equilibrium the two statistics are approximately
equal. Under the null hypothesis of no population stratification the trend test is
asymptotic  distribution with one degree of freedom.
distribution with one degree of freedom.
The idea is that the statistic is inflated by a factor  so that
so that 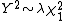 where
where  depends on the effect of stratification. The above method rests upon the assumptions that the inflation
depends on the effect of stratification. The above method rests upon the assumptions that the inflation
factor  is constant, which means that the loci should have roughly equal mutation
is constant, which means that the loci should have roughly equal mutation
rates, should not be under different selection in the two populations, and the amount of
Hardy-Weinberg disequilibrium measured in Wright’s coefficient of inbreeding F should
not differ between the different loci. The last of these is of greatest concern. If the effect of
the stratification is similar across the different loci  can be estimated from the unlinked
can be estimated from the unlinked
markers
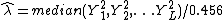
where L is the number of unlinked markers. The denominator
is derived from the gamma distribution as a robust estimator of  . Other estimators have been suggested, for example, Reich and Goldstein[8] suggested using the mean of the statistics instead.
. Other estimators have been suggested, for example, Reich and Goldstein[8] suggested using the mean of the statistics instead.
This is not the only way to estimate  but according to Bacanu et al.[9] it is an
but according to Bacanu et al.[9] it is an
appropriate estimate even if some of the unlinked markers are actually in disequilibrium
with a disease causing locus or are themselves associated with the disease. Under the
null hypothesis and when correcting for stratification using L unlinked genes, 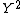 is
is
approximately 
distributed. With this correction the
overall type I error rate should be approximately equal to  even when the population
even when the population
is stratified.
Devlin and Roeder (1999)[10] mostly considered the situation where 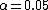 gives a
gives a
95% confidence level and not smaller p-values. Marchini et al. (2004)[11] demonstrates by
simulation that genomic control can lead to an anti-conservative p-value if this value
is very small and the two populations (case and control) are extremely distinct. This
was especially a problem if the number of unlinked markers were in the order 50 − 100.
This can result in false positives (at that significance level).
Demographic inference
Population structure is also an important aspect of evolutionary and population genetics. Many statistical methods rely on simple population models in order to infer historical demographic changes, such as the presence of population bottlenecks, admixture events or population divergence times. Often these methods rely on the assumption of panmictia, or homogeneity in an ancestral population. Recent studies have shown that the misspecification of such models, for instance by not taking into account the existence of structure in an ancestral population, can give rise to heavily biased parameter estimates.[12] Mounting evidence from simulation studies show that historical population structure can even have genetic effects that can easily be misinterpreted as historical changes in population size, or the existence of admixture events, even when no such events occurred.[13]
References
2. ^Devlin, B. and Roeder, K. (1999). Genomic control for association studies, Biometrics55(4): 997–1004.
3. ^Pritchard, JK, Stephens, M, Rosenberg NA, and Donnelly P. (2000) Association mapping in structured populations. American Journal of Human Genetics 67: 170-181
4. ^Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. (2006) Principal components analysis corrects for stratification in genome-wide association. Nature Genetics 38:904-909
5. ^Lander, E. S. and Schork, N. J. (1994). Genetic dissection of complex traits, Science 265(5181): 2037–2048.
6. ^Devlin, B. and Roeder, K. (1999). Genomic control for association studies, Biometrics55(4): 997–1004.
7. ^Bacanu, S.-A., Devlin, B. and Roeder, K. (2002). Association studies for quantitativetraits in structured populations, Genet Epidemiol 22(1): 78–93.
8. ^Reich, D. E. and Goldstein, D. B. (2001). Detecting association in a case-control study while correcting for population stratification, Genet Epidemiol 20(1): 4–16.
9. ^Bacanu, S. A., Devlin, B. and Roeder, K. (2000). The power of genomic control, Am JHum Genet 66(6): 1933–1944.
10. ^Devlin, B. and Roeder, K. (1999). Genomic control for association studies, Biometrics55(4): 997–1004.
11. ^Marchini, J., Cardon, L. R., Phillips, M. S. and Donnelly, P. (2004). The effects of humanpopulation structure on large genetic association studies, Nat Genet 36(5): 512–517.
12. ^{{Cite journal|last=Scerri|first=Eleanor M.L.|last2=Thomas|first2=Mark G.|last3=Manica|first3=Andrea|last4=Gunz|first4=Philipp|last5=Stock|first5=Jay T.|last6=Stringer|first6=Chris|last7=Grove|first7=Matt|last8=Groucutt|first8=Huw S.|last9=Timmermann|first9=Axel|date=August 2018|title=Did Our Species Evolve in Subdivided Populations across Africa, and Why Does It Matter?|url=https://linkinghub.elsevier.com/retrieve/pii/S0169534718301174|journal=Trends in Ecology & Evolution|volume=33|issue=8|pages=582–594|doi=10.1016/j.tree.2018.05.005}}
13. ^{{Cite journal|last=Rodríguez|first=Willy|last2=Mazet|first2=Olivier|last3=Grusea|first3=Simona|last4=Arredondo|first4=Armando|last5=Corujo|first5=Josué M.|last6=Boitard|first6=Simon|last7=Chikhi|first7=Lounès|date=December 2018|title=The IICR and the non-stationary structured coalescent: towards demographic inference with arbitrary changes in population structure|url=http://www.nature.com/articles/s41437-018-0148-0|journal=Heredity|volume=121|issue=6|pages=663–678|doi=10.1038/s41437-018-0148-0|issn=0018-067X|pmc=6221895|pmid=30293985}}
- List of United States Supreme Court cases, volume 422
- List of United States Supreme Court cases, volume 423
- List of United States Supreme Court cases, volume 424
- List of United States Supreme Court cases, volume 425
- List of United States Supreme Court cases, volume 426
- List of United States Supreme Court cases, volume 427
- List of United States Supreme Court cases, volume 428
- List of United States Supreme Court cases, volume 429
- List of United States Supreme Court cases, volume 43
- List of United States Supreme Court cases, volume 430
- List of United States Supreme Court cases, volume 431
- List of United States Supreme Court cases, volume 432
- List of United States Supreme Court cases, volume 433
- List of United States Supreme Court cases, volume 434
- List of United States Supreme Court cases, volume 435
- List of United States Supreme Court cases, volume 436
- List of United States Supreme Court cases, volume 437
- List of United States Supreme Court cases, volume 438
- List of United States Supreme Court cases, volume 439
- List of United States Supreme Court cases, volume 44
- List of United States Supreme Court cases, volume 440
- List of United States Supreme Court cases, volume 441
- List of United States Supreme Court cases, volume 442
- List of United States Supreme Court cases, volume 443
- List of United States Supreme Court cases, volume 444