“Mackey space”的意思、由来-开放百科全书

词条

Mackey space

释义

Examples
Properties
References

In mathematics, particularly in functional analysis, a Mackey space is a locally convex topological vector space X such that the topology of X coincides with the Mackey topology τ(X,X′), the finest topology which still preserves the continuous dual.

Examples

Examples of Mackey spaces include:

All bornological spaces.
All Hausdorff locally convex quasi-barrelled (and hence all Hausdorff locally convex barrelled spaces and all Hausdorff locally convex reflexive spaces).
All Hausdorff locally convex metrizable spaces.^[1]
All Hausdorff locally convex barreled spaces.^[1]
The product, locally convex direct sum, and the inductive limit of a family of Mackey spaces is a Mackey space.^[2]

Properties

A locally convex space with continuous dual is a Mackey space if and only if each convex and 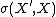-relatively compact subset of is equicontinuous.
The completion of a Mackey space is again a Mackey space.^[3]
A separated quotient of a Mackey space is again a Mackey space.
A Mackey space need not be separable, complete, quasi-barrelled, nor -quasi-barrelled.

References

1. ^¹Schaefer (1999) p. 132
2. ^Schaefer (1999) p. 138
3. ^Schaefer (1999) p. 133

{{cite book |last=Robertson |first=A.P. |author2=W.J. Robertson |title= Topological vector spaces |series=Cambridge Tracts in Mathematics |volume=53 |year=1964 |publisher= Cambridge University Press | page=81 }}
{{cite book | author=H.H. Schaefer | title=Topological Vector Spaces | publisher=Springer-Verlag | series=GTM | volume=3 | date=1970 | isbn=0-387-05380-8 | pages=132–133 }}
{{cite book | author=S.M. Khaleelulla | title=Counterexamples in Topological Vector Spaces | publisher=Springer-Verlag | series=GTM | volume=936 | date=1982 | isbn=978-3-540-11565-6 | pages=31, 41, 55-58 }}

1 : Topological vector spaces

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。