- Definition
- Examples
- See also
- Applications
- References
In functional analysis and related areas of mathematics, the Mackey topology, named after George Mackey, is the finest topology for a topological vector space which still preserves the continuous dual. In other words the Mackey topology does not make linear functions continuous which were discontinuous in the default topology.
The Mackey topology is the opposite of the weak topology, which is the coarsest topology on a topological vector space which preserves the continuity of all linear functions in the continuous dual.
The Mackey–Arens theorem states that all possible dual topologies are finer than the weak topology and coarser than the Mackey topology.
Definition
Given a dual pair 
with 
a topological vector space and 
its continuous dual the Mackey topology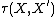 
is a polar topology defined on by using the set of all absolutely convex and weakly compact sets in .
Examples
- Every metrisable locally convex space
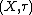with continuous dual carries the Mackey topology, that is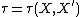 
, or to put it more succinctly every metrisable locally convex space is a Mackey space. - Every Fréchet space 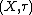carries the Mackey topology and the topology coincides with the strong topology, that is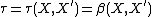
See also
- Polar topology
- Weak topology
- Strong topology
Applications
The Mackey topology has an application in economies with infinitely many commodities.[1]
References
- {{springer|id=M/m062080|title=Mackey topology|author=A.I. Shtern}}
- {{cite journal | last=Mackey | first=G.W. | authorlink=George Mackey | title=On convex topological linear spaces | journal=Trans. Amer. Math. Soc. | volume=60 | year=1946 | pages=519–537 | doi=10.2307/1990352 | issue=3 | publisher=Transactions of the American Mathematical Society, Vol. 60, No. 3 | jstor=1990352 | pmc=1078658 }}
- {{cite book | last=Bourbaki | first=Nicolas | authorlink=Nicolas Bourbaki | title=Topological vector spaces | series=Elements of mathematics | publisher=Addison–Wesley | year=1977 }}
- {{cite book |last=Robertson |first=A.P. |author2=W.J. Robertson |title= Topological vector spaces |series=Cambridge Tracts in Mathematics |volume=53 |year=1964 |publisher= Cambridge University Press | page=62}}
- {{cite book | last = Schaefer | first = Helmuth H. | year = 1971 | title = Topological vector spaces | series=GTM | volume=3 | publisher = Springer-Verlag | location = New York | isbn = 0-387-98726-6 | page=131 }}
- That's My Bush
- That's My Bush!
- That's My Mama
- That Sri Song Hak
- That's So Not Raven
- That's So Raven
- That's So Raven (soundtrack)
- ...That's the Way It Is
- That's the Way Love Goes (Janet Jackson song)
- That's the Way Love Is (The Isley Brothers song)
- That's the Way of the World
- That's the way to do it!
- That's the way to do it
- That Stubborn Kinda Fellow
- That's What Friends Are For
- That's What I'm Talking About
- That's Why I'm Here
- Thatta
- That Thing You Do!
- That Thing You Do (song)
- . . . That Thou Art Mindful of Him
- That Thou art Mindful of Him
- That Thou Art Mindful of Him
- That Touch of Mink
- That Uncertain Feeling (novel)