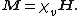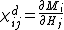请输入您要查询的百科知识：

　

词条 Magnetic susceptibility
释义

  1. Definition

      Volume susceptibility    Mass susceptibility and molar susceptibility    In CGS units  

  2. Paramagnetism and diamagnetism

  3. Experimental measurement

  4. Tensor susceptibility

  5. Differential susceptibility

  6. In the frequency domain

  7. Examples

  8. Sources of confusion in published data

  9. See also

  10. References and notes

  11. External links

{{Technical|date=April 2015}}

In electromagnetism, the magnetic susceptibility (Latin: {{lang|la|susceptibilis}}, "receptive"; denoted {{mvar|{{nounderlines|χ}}}}) is a measure of how much a material will become magnetized in an applied magnetic field. Mathematically, it is the ratio of magnetization {{math|M}} (magnetic moment per unit volume) to the applied magnetizing field intensity {{math|H}}. This allows a simple classification of most materials' response to an applied magnetic field into two categories: an alignment with the magnetic field, χ>0, called paramagnetism, or an alignment against the field, χ<0, called diamagnetism.

This alignment has several effects. First, the magnetic susceptibility indicates whether a material is attracted into or repelled out of a magnetic field. Paramagnetic materials align with the field, so are attracted to the magnetic field. Diamagnetic materials are anti-aligned, so are pushed away from magnetic fields. Second, on top of the applied field, the magnetic moment of the material adds its own magnetic field, causing the field lines to concentrate in paramagnetism, or be excluded in diamagnetism.[1] Quantitative measures of the magnetic susceptibility also provide insights into the structure of materials, providing insight into bonding and energy levels.

Fundamentally, the magnetic moment of materials comes from the magnetism of the particles they are made of. Usually, this is dominated by the magnetic moments of electrons. Electrons are present in all materials, but without any external magnetic field, the magnetic moments of the electrons are usually in some way either paired up or randomized so the overall magnetism is zero.(the exception to this usual case is ferromagnetism) The fundamental reasons why the magnetic moments of the electrons line up or don't can be very complex, and can not be explained with classical physics. However, it is a useful simplification to simply measure the magnetic susceptibility of a material, and apply the macroscopic form of Maxwell's equations. This allows classical physics to make useful predictions without getting into the underlying quantum mechanical details.

Definition

{{see also|Permeability (electromagnetism)#Relative permeability and magnetic susceptibility}}

Volume susceptibility

Magnetic susceptibility is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field. A related term is magnetizability, the proportion between magnetic moment and magnetic flux density.[2] A closely related parameter is the permeability, which expresses the total magnetization of material and volume.

The volume magnetic susceptibility, represented by the symbol {{mvar|χv}} (often simply {{mvar|χ}}, sometimes {{mvar|χm}} – magnetic, to distinguish from the electric susceptibility), is defined in the International System of Units — in other systems there may be additional constants — by the following relationship:[3]

Here

  • {{math|M}} is the magnetization of the material (the magnetic dipole moment per unit volume), measured in amperes per meter, and
  • {{math|H}} is the magnetic field strength, also measured in amperes per meter.
{{mvar|χv}} is therefore a dimensionless quantity.

Using SI units, the magnetic induction {{math|B}} is related to {{math|H}} by the relationship

where {{math|μ0}} is the vacuum permeability (see table of physical constants), and {{math|(1 + χv)}} is the relative permeability of the material. Thus the volume magnetic susceptibility {{mvar|χv}} and the magnetic permeability {{mvar|μ}} are related by the following formula:

Sometimes[4] an auxiliary quantity called intensity of magnetization {{math|I}} (also referred to as magnetic polarisation {{math|J}}) and measured in teslas, is defined as

This allows an alternative description of all magnetization phenomena in terms of the quantities {{math|I}} and {{math|B}}, as opposed to the commonly used {{math|M}} and {{math|H}}.

Mass susceptibility and molar susceptibility

There are two other measures of susceptibility, the mass magnetic susceptibility ({{math|χmass}} or {{math|χg}}, sometimes {{math|χm}}), measured in m3/kg (SI) and the molar magnetic susceptibility ({{math|χmol}}) measured in m3/mol that are defined below, where {{mvar|ρ}} is the density in kg/m3 and {{mvar|M}} is molar mass in kg/mol:

;

.

In CGS units

Note that the definitions above are according to SI conventions. However, many tables of magnetic susceptibility give cgs values (more specifically emu-cgs, short for electromagnetic units, or Gaussian-cgs; both are the same in this context). These units rely on a different definition of the permeability of free space:[5]

The dimensionless cgs value of volume susceptibility is multiplied by 4{{pi}} to give the dimensionless SI volume susceptibility value:[5]

For example, the cgs volume magnetic susceptibility of water at 20 °C is {{val|-7.19e-7}}, which is {{val|-9.04e-6}} using the SI convention.

In physics it is common to see cgs mass susceptibility given in cm3/g or emu/g·Oe−1, so to convert to SI volume susceptibility we use the conversion [6]

where {{math|ρcgs}} is the density given in g/cm3, or

.

The molar susceptibility is measured cm3/mol or emu/mol·Oe−1 in cgs and is calculated using the molar mass in g/mol.

Paramagnetism and diamagnetism

If {{mvar|χ}} is positive, a material can be paramagnetic. In this case, the magnetic field in the material is strengthened by the induced magnetization. Alternatively, if {{mvar|χ}} is negative, the material is diamagnetic. In this case, the magnetic field in the material is weakened by the induced magnetization. Generally, nonmagnetic materials are said to be para- or diamagnetic because they do not possess permanent magnetization without external magnetic field. Ferromagnetic, ferrimagnetic, or antiferromagnetic materials possess permanent magnetization even without external magnetic field and do not have a well defined zero-field susceptibility.

Experimental measurement

Volume magnetic susceptibility is measured by the force change felt upon a substance when a magnetic field gradient is applied.[7] Early measurements are made using the Gouy balance where a sample is hung between the poles of an electromagnet. The change in weight when the electromagnet is turned on is proportional to the susceptibility. Today, high-end measurement systems use a superconductive magnet. An alternative is to measure the force change on a strong compact magnet upon insertion of the sample. This system, widely used today, is called the Evans balance.[8] For liquid samples, the susceptibility can be measured from the dependence of the NMR frequency of the sample on its shape or orientation.[9][10][11][12][13]

Another method using NMR techniques measures the magnetic field distortion around a sample immersed in water inside an MR scanner. This method is highly accurate for diamagnetic materials with susceptibilities similar to water.[14]

Tensor susceptibility

The magnetic susceptibility of most crystals is not a scalar quantity. Magnetic response {{math|M}} is dependent upon the orientation of the sample and can occur in directions other than that of the applied field {{math|H}}. In these cases, volume susceptibility is defined as a tensor

where {{mvar|i}} and {{mvar|j}} refer to the directions (e.g., {{mvar|x}} and {{mvar|y}} in Cartesian coordinates) of the applied field and magnetization, respectively. The tensor is thus rank 2 (second order), dimension (3,3) describing the component of magnetization in the {{mvar|i}}th direction from the external field applied in the {{mvar|j}}th direction.

Differential susceptibility

In ferromagnetic crystals, the relationship between {{math|M}} and {{math|H}} is not linear. To accommodate this, a more general definition of differential susceptibility is used

where {{math|χ{{su|p=d|b=ij}}}} is a tensor derived from partial derivatives of components of {{math|M}} with respect to components of {{math|H}}. When the coercivity of the material parallel to an applied field is the smaller of the two, the differential susceptibility is a function of the applied field and self interactions, such as the magnetic anisotropy. When the material is not saturated, the effect will be nonlinear and dependent upon the domain wall configuration of the material.

Several experimental techniques allow for the measurement of the electronic properties of a material. An important effect in metals under strong magnetic fields, is the oscillation of the differential susceptibility as function of 1/H. This behaviour is known as the de Haas–van Alphen effect and relates the period of the susceptibility with the Fermi surface of the material.

In the frequency domain

When the magnetic susceptibility is measured in response to an AC magnetic field (i.e. a magnetic field that varies sinusoidally), this is called AC susceptibility. AC susceptibility (and the closely related "AC permeability") are complex number quantities, and various phenomena, such as resonance, can be seen in AC susceptibility that cannot in constant-field (DC) susceptibility. In particular, when an AC field is applied perpendicular to the detection direction (called the "transverse susceptibility" regardless of the frequency), the effect has a peak at the ferromagnetic resonance frequency of the material with a given static applied field. Currently, this effect is called the microwave permeability or network ferromagnetic resonance in the literature. These results are sensitive to the domain wall configuration of the material and eddy currents.

In terms of ferromagnetic resonance, the effect of an AC-field applied along the direction of the magnetization is called parallel pumping.

Examples

Magnetic susceptibility of some materials
MaterialTemp.|Temperature PressureMolar {{abbr|susc.|susceptibility, {{math|χmolMass {{abbr|susc.|susceptibility, {{math|χmassVolume {{abbr|susc.|susceptibility, {{math|χvM Density,
(°C)(atm)SI
(m3/mol)		CGS
(cm3/mol)		SI
(m3/kg)		CGS
(cm3/g)		SI
CGS
(emu)		{{nowrap|(10−3 kg/mol
{{nowrap|{{= g/mol)		{{nowrap|(103 kg/m3
{{nowrap|{{= g/cm3)
Helium[15] 20 1 -2.38e-11}}-1.89e-6}}-5.93e-9}}-4.72e-7}}-9.85e-10}}-7.84e-11}} 4.0026 1.66e-4}}
Xenon[15] 20 1 -5.71e-10}}-4.54e-5}}-4.35e-9}}-3.46e-7}}-2.37e-8}}-1.89e-9}} 131.29 5.46e-3}}
Oxygen[15] 20 0.209 +4.3e-8}}+3.42e-3}}+1.34e-6}}+1.07e-4}}+3.73e-7}}+2.97e-8}} 31.99 2.78e-4}}
Nitrogen[15] 20 0.781 -1.56e-10}}-1.24e-5}}-5.56e-9}}-4.43e-7}}-5.06e-9}}-4.03e-10}} 28.01 9.10e-4}}
Air (NTP)[16] 20 1 +3.6e-7}}+2.9e-8}} 28.97 1.29e-3}}
Water[17] 20 1 -1.631e-10}}-1.298e-5}}-9.051e-9}}-7.203e-7}}-9.035e-6}}-7.190e-7}} 18.015 0.9982
Paraffin oil, 220–260{{nbsp}}cSt[14] 22 1-1.01e-8}}-8.0e-7}}-8.8e-6}}-7.0e-7}} 0.878
PMMA[14] 22 1-7.61e-9}}-6.06e-7}}-9.06e-6}}-7.21e-7}} 1.190
PVC[14] 22 1-7.80e-9}}-6.21e-7}}-1.071e-5}}-8.52e-7}} 1.372
Fused silica glass[14] 22 1-5.12e-9}}-4.07e-7}}-1.128e-5}}-8.98e-7}} 2.20
Diamond[18] r.t. 1 -7.4e-11}}-5.9e-6}}-6.2e-9}}-4.9e-7}}-2.2e-5}}-1.7e-6}} 12.01 3.513
Graphite[19] {{math|χ∥}} (to c-axis) r.t. 1 -7.5e-11}}-6.0e-6}}-6.3e-9}}-5.0e-7}}-1.4e-5}}-1.1e-6}} 12.01 2.267
Graphite[19] {{math|χ∥}} r.t. 1 -3.2e-9}}-2.6e-4}}-2.7e-7}}-2.2e-5}}-6.1e-4}}-4.9e-5}} 12.01 2.267
Graphite[19] {{math|χ∥}} −173 1 -4.4e-9}}-3.5e-4}}-3.6e-7}}-2.9e-5}}-8.3e-4}}-6.6e-5}} 12.01 2.267
Aluminium[20] 1 +2.2e-10}}+1.7e-5}}+7.9e-9}}+6.3e-7}}+2.2e-5}}+1.75e-6}} 26.98 2.70
Silver[21] 961 1 -2.31e-5}}-1.84e-6}} 107.87
Bismuth[22] 20 1 -3.55e-9}}-2.82e-4}}-1.70e-8}}-1.35e-6}}-1.66e-4}}-1.32e-5}} 208.98 9.78
Copper[16] 20 1 -1.0785e-9}}-9.63e-6}}-7.66e-7}} 63.546 8.92
Nickel[16] 20 1 600 48 58.69 8.9
Iron[16] 20 1 200000}}15900}} 55.847 7.874

Sources of confusion in published data

The CRC Handbook of Chemistry and Physics has one of the only published magnetic susceptibility tables. Some of the data (e.g., for aluminium, bismuth, and diamond) is listed as cgs, which has caused confusion to some readers. "cgs" is an abbreviation of centimeters–grams–seconds; it represents the form of the units, but cgs does not specify units. Correct units of magnetic susceptibility in cgs is cm3/mol or cm3/g. Molar susceptibility and mass susceptibility are both listed in the CRC. Some table have listed magnetic susceptibility of diamagnets as positives. It is important to check the header of the table for the correct units and sign of magnetic susceptibility readings.

See also

{{div col|colwidth=20em}}
  • Curie constant
  • Electric susceptibility
  • Iron
  • Magnetic constant
  • Magnetic flux density
  • Magnetism
  • Magnetochemistry
  • Magnetometer
  • Maxwell's equations
  • Paleomagnetism
  • Permeability (electromagnetism)
  • Quantitative susceptibility mapping
  • Susceptibility weighted imaging
{{div col end}}

References and notes

1. ^Roger Grinter, The Quantum in Chemistry: An Experimentalist's View, John Wiley & Sons, 2005, {{ISBN|0470017627}} page 364
2. ^{{cite encyclopedia |year=1997 |title =magnetizability, {{mvar|ξ}} |encyclopedia=IUPAC Compendium of Chemical Terminology—The Gold Book |publisher=International Union of Pure and Applied Chemistry |edition=2nd |url=http://goldbook.iupac.org/search.py?search_text=magnetizability}}
3. ^{{cite book|last1=O'Handley|first1=Robert C.|title=Modern Magnetic Materials|date=2000|publisher=Wiley|location=Hoboken, NJ|isbn=9780471155669}}
4. ^{{cite web|author=Richard A. Clarke |url=http://info.ee.surrey.ac.uk/Workshop/advice/coils/mu/#itns |title=Magnetic properties of materials |publisher=Info.ee.surrey.ac.uk |date= |accessdate=2011-11-08}}
5. ^1 {{cite journal|author1=Bennett, L. H.|author2=Page, C. H.|author3=Swartzendruber, L. J.|last-author-amp=yes|year=1978|title=Comments on units in magnetism|journal=Journal of Research of the National Bureau of Standards|publisher=NIST, USA|volume=83|issue=1|pages=9–12|doi=10.6028/jres.083.002}}
6. ^{{cite web|url=http://www.ieeemagnetics.org/index.php?option=com_content&view=article&id=118&Itemid=107|title=IEEE Magnetic unit conversions}}
7. ^{{cite book| author=L. N. Mulay| title=Techniques of Chemistry|editor1=A. Weissberger |editor2=B. W. Rossiter | publisher=Wiley-Interscience: New York| volume=4| page = 431| year=1972}}
8. ^{{cite web|url=http://www.sherwood-scientific.com/msb/msbindex.html |title=Magnetic Susceptibility Balances |publisher=Sherwood-scientific.com |date= |accessdate=2011-11-08}}
9. ^{{ cite journal| author=J. R. Zimmerman, and M. R. Foster| title=Standardization of NMR high resolution spectra| journal=J. Phys. Chem.| volume=61| year=1957| pages=282–289| doi=10.1021/j150549a006| issue=3}}
10. ^{{cite journal|author1=Robert Engel |author2=Donald Halpern |author3=Susan Bienenfeld |last-author-amp=yes | title=Determination of magnetic moments in solution by nuclear magnetic resonance spectrometry| journal=Anal. Chem.| volume=45| year=1973| pages=367–369| doi=10.1021/ac60324a054| issue=2}}
11. ^{{cite journal|author1=P. W. Kuchel |author2=B. E. Chapman |author3=W. A. Bubb |author4=P. E. Hansen |author5=C. J. Durrant |author6=M. P. Hertzberg |last-author-amp=yes | title=Magnetic susceptibility: solutions, emulsions, and cells| journal=Concepts Magn. Reson.| volume=A 18| year=2003| pages=56–71| doi=10.1002/cmr.a.10066|arxiv=q-bio/0601030}}
12. ^{{cite journal|author1=K. Frei |author2=H. J. Bernstein |lastauthoramp=yes | title=Method for determining magnetic susceptibilities by NMR| journal=J. Chem. Phys.| volume=37| year=1962| pages=1891–1892| doi=10.1063/1.1733393|bibcode = 1962JChPh..37.1891F| issue=8 }}
13. ^{{cite journal| author=R. E. Hoffman| title=Variations on the chemical shift of TMS| journal=J. Magn. Reson.| volume=163| year=2003| pages=325–331| doi=10.1016/S1090-7807(03)00142-3| pmid=12914848| issue=2|bibcode = 2003JMagR.163..325H }}
14. ^1 2 3 4 {{cite journal|last1=Wapler|first1=M. C.|last2=Leupold|first2=J.|last3=Dragonu|first3=I.|last4=von Elverfeldt|first4=D.|last5=Zaitsev|first5=M.|last6=Wallrabe|first6=U.|title=Magnetic properties of materials for MR engineering, micro-MR and beyond|journal=JMR|date=2014|volume=242|pages=233–242|doi=10.1016/j.jmr.2014.02.005|pmid=24705364|arxiv=1403.4760|bibcode=2014JMagR.242..233W}}
15. ^1 2 3 {{cite journal | author = R. E. Glick | title = On the Diamagnetic Susceptibility of Gases | year = 1961 | journal = J. Phys. Chem. | volume = 65 | issue = 9 | pages = 1552–1555 | doi = 10.1021/j100905a020}}
16. ^1 2 3  {{cite journal | author = John F. Schenck | title = The role of magnetic susceptibility in magnetic resonance imaging: MRI magnetic compatibility of the first and second kinds | year = 1993 | journal = Medical Physics | volume = 23 | issue = 6 | pages = 815–850 | doi = 10.1118/1.597854 | pmid=8798169|bibcode = 1996MedPh..23..815S }}
17. ^ {{cite journal | author1=G. P. Arrighini | author2=M. Maestro | author3=R. Moccia | last-author-amp=yes | title=Magnetic Properties of Polyatomic Molecules: Magnetic Susceptibility of H2O, NH3, CH4, H2O2 | journal=J. Chem. Phys. | volume=49 | year=1968 | pages=882–889 | doi=10.1063/1.1670155|bibcode = 1968JChPh..49..882A | issue=2 }}
18. ^{{cite journal | author = J. Heremans, C. H. Olk and D. T. Morelli | title = Magnetic Susceptibility of Carbon Structures | year = 1994 | journal = Phys. Rev. B | volume = 49 | issue = 21 | pages = 15122–15125 | doi = 10.1103/PhysRevB.49.15122 | bibcode = 1994PhRvB..4915122H}}
19. ^1 2  {{cite journal | author1=N. Ganguli | author2=K.S. Krishnan | lastauthoramp=yes | title = The Magnetic and Other Properties of the Free Electrons in Graphite | year = 1941 | journal = Proceedings of the Royal Society | volume = 177 | issue = 969 | pages = 168–182 | doi = 10.1098/rspa.1941.0002 | bibcode = 1941RSPSA.177..168G | url=http://rspa.royalsocietypublishing.org/content/royprsa/177/969/168.full.pdf}}
20. ^{{Cite web|url=http://hyperphysics.phy-astr.gsu.edu/Hbase/tables/magprop.html|title=Magnetic Properties of Solids|last=Nave|first=Carl L|work=HyperPhysics|accessdate=2008-11-09}}
21. ^ {{cite journal |author1=R. Dupree |author2=C. J. Ford |lastauthoramp=yes | title = Magnetic susceptibility of the noble metals around their melting points | year = 1973 | journal = Phys. Rev. B | volume = 8 | issue = 4 | pages = 1780–1782 | doi = 10.1103/PhysRevB.8.1780|bibcode = 1973PhRvB...8.1780D }}
22. ^ {{cite journal |author1=S. Otake, M. Momiuchi |author2=N. Matsuno |lastauthoramp=yes | title = Temperature Dependence of the Magnetic Susceptibility of Bismuth | year = 1980 | journal = J. Phys. Soc. Jpn. | volume = 49 | issue = 5 | pages = 1824–1828 | doi = 10.1143/JPSJ.49.1824|bibcode = 1980JPSJ...49.1824O }} The tensor needs to be averaged over all orientations: {{math|χ {{=}} {{sfrac|1|3}}χ∥ + {{sfrac|2|3}}χ⊥}}.

External links

  • Linear Response Functions in Eva Pavarini, Erik Koch, Dieter Vollhardt, and Alexander Lichtenstein (eds.): DMFT at 25: Infinite Dimensions, Verlag des Forschungszentrum Jülich, 2014 {{ISBN|978-3-89336-953-9}}
{{DEFAULTSORT:Magnetic Susceptibility}}

4 : Physical quantities|Magnetism|Electric and magnetic fields in matter|Scientific techniques
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/11 8:18:53