- Existence
- Non-uniqueness
- Construction Rank factorization from row echelon forms Example Proof Singular value decomposition
- Consequences rank(A) = rank(AT)
- Notes
- References
Given an  matrix
matrix  of rank
of rank  , a rank decomposition or rank factorization of
, a rank decomposition or rank factorization of  is a product
is a product  , where
, where  is an
is an 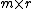 matrix and
matrix and  is an
is an 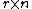 matrix.
matrix.
Existence
Every finite-dimensional matrix has a rank decomposition: Let  be an
be an  matrix whose column rank is
matrix whose column rank is  . Therefore, there are
. Therefore, there are  linearly independent columns in
linearly independent columns in  ; equivalently, the dimension of the column space of
; equivalently, the dimension of the column space of  is
is  . Let
. Let  be any basis for the column space of
be any basis for the column space of  and place them as column vectors to form the
and place them as column vectors to form the  matrix
matrix 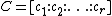 . Therefore, every column vector of
. Therefore, every column vector of  is a linear combination of the columns of
is a linear combination of the columns of  . To be precise, if
. To be precise, if  is an
is an  matrix with
matrix with  as the
as the  -th column, then
-th column, then
where  's are the scalar coefficients of
's are the scalar coefficients of  in terms of the basis
in terms of the basis  . This implies that
. This implies that  , where
, where  is the
is the  -th element of
-th element of  .
.
Non-uniqueness
If  is rank factorization, taking
is rank factorization, taking  and
and
 gives another rank factorization for any invertible matrix
gives another rank factorization for any invertible matrix  of compatible dimensions.
of compatible dimensions.
Conversely, if 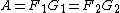 are two rank factorizations of
are two rank factorizations of  , then there exists an invertible matrix
, then there exists an invertible matrix  such that
such that  and
and  .[1]
.[1]
Construction
Rank factorization from row echelon forms
In practice, we can construct one specific rank factorization as follows: we can compute  , the reduced row echelon form of
, the reduced row echelon form of  . Then
. Then  is obtained by removing from
is obtained by removing from  all non-pivot columns, and
all non-pivot columns, and  by eliminating all zero rows of
by eliminating all zero rows of  .
.
Example
Consider the matrix
 is in reduced echelon form.
is in reduced echelon form.
Then  is obtained by removing the third column of
is obtained by removing the third column of  , the only one which is not a pivot column, and
, the only one which is not a pivot column, and  by getting rid of the last row of zeroes, so
by getting rid of the last row of zeroes, so
It is straightforward to check that
Proof
Let  be an
be an  permutation matrix such that
permutation matrix such that  in block partitioned form, where the columns of
in block partitioned form, where the columns of  are the
are the  pivot columns of
pivot columns of  . Every column of
. Every column of  is a linear combination of the columns of
is a linear combination of the columns of  , so there is a matrix
, so there is a matrix 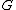 such that
such that  , where the columns of
, where the columns of 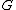 contain the coefficients of each of those linear combinations. So
contain the coefficients of each of those linear combinations. So  ,
,  being the
being the  identity matrix. We will show now that
identity matrix. We will show now that  .
.
Transforming 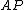 into its reduced row echelon form amounts to left-multiplying by a matrix
into its reduced row echelon form amounts to left-multiplying by a matrix  which is a product of elementary matrices, so
which is a product of elementary matrices, so  , where
, where  . We then can write
. We then can write  , which allows us to identify
, which allows us to identify  , i.e. the nonzero
, i.e. the nonzero  rows of the reduced echelon form, with the same permutation on the columns as we did for
rows of the reduced echelon form, with the same permutation on the columns as we did for  . We thus have
. We thus have 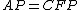 , and since
, and since  is invertible this implies
is invertible this implies  , and the proof is complete.
, and the proof is complete.
Singular value decomposition
One can also construct a full rank factorization of  by using its singular value decomposition
by using its singular value decomposition
Since 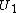 is a full column rank matrix and
is a full column rank matrix and  is a full row rank matrix, we can take
is a full row rank matrix, we can take  and
and 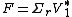 .
.
Consequences
rank(A) = rank(AT)
An immediate consequence of rank factorization is that the rank of  is equal to the rank of its transpose
is equal to the rank of its transpose 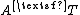 . Since the columns of
. Since the columns of  are the rows of
are the rows of 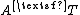 , the column rank of
, the column rank of  equals its row rank.
equals its row rank.
Proof: To see why this is true, let us first define rank to mean column rank. Since  , it follows that
, it follows that  . From the definition of matrix multiplication, this means that each column of
. From the definition of matrix multiplication, this means that each column of 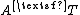 is a linear combination of the columns of
is a linear combination of the columns of 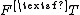 . Therefore, the column space of
. Therefore, the column space of 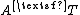 is contained within the column space of
is contained within the column space of 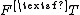 and, hence, rank
and, hence, rank ≤ rank
≤ rank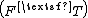 .
.
Now, 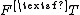 is
is  , so there are
, so there are  columns in
columns in 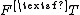 and, hence, rank
and, hence, rank ≤
≤  = rank
= rank . This proves that rank
. This proves that rank ≤ rank
≤ rank .
.
Now apply the result to 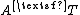 to obtain the reverse inequality: since
to obtain the reverse inequality: since  =
=  , we can write rank
, we can write rank = rank
= rank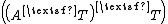 ≤ rank
≤ rank . This proves rank
. This proves rank ≤ rank
≤ rank .
.
We have, therefore, proved rank ≤ rank
≤ rank and rank
and rank ≤ rank
≤ rank , so rank
, so rank = rank
= rank . (Also see the first proof of column rank = row rank under rank).
. (Also see the first proof of column rank = row rank under rank).
Notes
References
{{refbegin}}- {{Citation | last = Banerjee | first = Sudipto | last2 = Roy | first2 = Anindya | date = 2014 | title = Linear Algebra and Matrix Analysis for Statistics | series = Texts in Statistical Science | publisher = Chapman and Hall/CRC | edition = 1st | isbn = 978-1420095388}}
- {{Citation | last = Lay | first = David C. | date = 2005 | title = Linear Algebra and its Applications | publisher = Addison Wesley | edition = 3rd | isbn = 978-0-201-70970-4}}
- {{Citation | last = Golub | first = Gene H. | last2 = Van Loan | first2 = Charles F. | date = 1996 | title = Matrix Computations | series = Johns Hopkins Studies in Mathematical Sciences | publisher = The Johns Hopkins University Press | edition = 3rd | isbn = 978-0-8018-5414-9}}
- {{Citation | last = Stewart | first = Gilbert W. | date = 1998 | title = Matrix Algorithms. I. Basic Decompositions | publisher = SIAM | isbn = 978-0-89871-414-2}}
- {{cite journal|last1=Piziak|first1=R.|last2=Odell|first2=P. L.|title=Full Rank Factorization of Matrices|journal=Mathematics Magazine|date=1 June 1999|volume=72|issue=3|pages=193|doi=10.2307/2690882}}
- Beatrice Whiting
- Beatrice Willard
- Beatrice Willard Alpine Tundra Research Plots
- Beatrice Williams
- Beatrice Winser
- Beatrice Worsley
- Beatrice Wright (psychologist)
- Beatrijs (Dutch magazine)
- Beatrijs (magazine)
- Beatrix Bloxam
- Beatrix bloxam
- Beatrix da Silva
- Beatrix de Courtenay
- Beatrix de Cusance
- Beatrix de Rijke
- Beatrix de Vesci
- Beatrix D'Souza
- Beatrix (Final Fantasy IX)
- Beatrix Hamburg
- Beatrix Mullner
- Beatrix Müllner
- Beatrix of Andechs-Merania
- Beatrix of Baden
- Beatrix of Bar
- Beatrix of Brandenburg




