“Raynaud surface”的意思、由来-开放百科全书

词条

Raynaud surface

释义

References

In mathematics, a Raynaud surface is a particular kind of algebraic surface that was introduced in {{harvs|txt|last=Lang|first=William E.|year=1979}} and named for {{harvs|txt|last=Raynaud|first=Michel|authorlink=Michel Raynaud|year=1978}}. To be precise, a Raynaud surface is a quasi-elliptic surface over an algebraic curve of genus g greater than 1, such that all fibers are irreducible and the fibration has a section. The Kodaira vanishing theorem fails for such surfaces; in other words the Kodaira theorem, valid in algebraic geometry over the complex numbers, has such surfaces as counterexamples, and these can only exist in characteristic p.

Generalized Raynaud surfaces were introduced in {{harv|Lang|1983}}, and give examples of surfaces of general type with global vector fields.

References

{{Citation | last1=Lang | first1=William E. | title=Quasi-elliptic surfaces in characteristic three | url=http://www.numdam.org/item?id=ASENS_1979_4_12_4_473_0 |mr=565468 | year=1979 | journal=Annales Scientifiques de l'École Normale Supérieure |series=Série 4 | issn=0012-9593 | volume=12 | issue=4 | pages=473–500}}
{{Citation | last1=Lang | first1=William E. | title=Arithmetic and geometry, Vol. II | publisher=Birkhäuser Boston | location=Boston, MA | series=Progress in Mathematics |mr=717611 | year=1983 | volume=36 | chapter=Examples of surfaces of general type with vector fields | pages=167–173}}
{{Citation | last1=Raynaud | first1=Michel | author1-link=Michel Raynaud | title=C. P. Ramanujam—a tribute | publisher=Springer-Verlag | location=Berlin, New York | series=Tata Inst. Fund. Res. Studies in Math. |mr=541027 | year=1978 | volume=8 | chapter=Contre-exemple au "vanishing theorem" en caractéristique 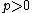| pages=273–278}}

1 : Algebraic surfaces

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。